Glasnik Matematicki, Vol. 39, No.2 (2004), 273--286.
ESTIMATES ON THE DIRICHLET HEAT KERNAL
OF DOMAINS ABOVE THE GRAPHS OF BOUNDED C1,1
FUNCTIONS
Renming Song
Department of Mathematics, University of Illinois,
Urbana, IL 61801, USA
e-mail: rsong@math.uiuc.edu
Abstract. Suppose that D is the domain in
Rd,
d ≥ 3, above the
graph of a bounded C1,1
function
Γ :
Rd-1
→ R
and that pD(t, x, y)
is the Dirichlet heat kernel in D. In
this paper we show that there exist positive constants
C1, C2,
C3, C4
such that for all t > 0 and
x, y
∈ D,
C1(ρ(x)ρ(y) / t
∧ 1)
t -d/2
e
-C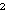 |x-y|^2
/ t
≤ pD(t, x, y),
|x-y|^2
/ t
≤ pD(t, x, y),
pD(t, x, y) ≤
C3(ρ(x)ρ(y) / t
∧ 1)
t -d/2
e
-C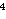 |x-y|^2
/ t,
|x-y|^2
/ t,
where ρ(x)
stands for the distance between x and
∂D.
2000 Mathematics Subject Classification.
35K05, 60J60, 60J45, 60J75.
Key words and phrases. Dirichlet heat kernels,
Green functions, killed Brownian motions.
Full text (PDF) (free access)
Glasnik Matematicki Home Page
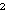 |x-y|^2
/ t
≤ pD(t, x, y),
|x-y|^2
/ t
≤ pD(t, x, y),
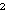 |x-y|^2
/ t
≤ pD(t, x, y),
|x-y|^2
/ t
≤ pD(t, x, y),
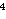 |x-y|^2
/ t,
|x-y|^2
/ t,