Glasnik Matematicki, Vol. 32, No.2 (1997), 263-273.
THE DIMENSION OF WHITNEY LEVELS OF A
FINITE GRAPH
Alejandro Illanes and Roberto Torres
Universidad Nacional Autonoma de Mexico, Instituto de Matematicas, Circuito Exterior, Ciudad Universitaria,
Mexico D.F. 04510, Mexico
Universidad Autonoma de Queretaro, Facultad de Ingenieria,
Cerro de las Campanas S/N, Col. Las Campanas,
Centro Universitario, Queretaro 76010, Mexico
Abstract. Let X be a finite connected graph
and let C(X) be the hyperspace of all subcontinua
of X. After establishing some basic facts about the
dimension of Whitney levels for C(X), we obtain
combinatoric characterizations of the families of graphs X
such that:
All the Whitney levels for C(X)
are of the same dimension.
Large Whitney levels for C(X) are
dimensionally homogeneous.
There exists a Whitney level for C(X)
which is homeomorphic to an n-cube.
We also prove that: Given a polyhedron
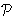 ,
there exist only finitely many X such that
,
there exist only finitely many X such that
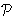 is homeomorphic to a
positive Whitney level for C(X).
is homeomorphic to a
positive Whitney level for C(X).
1991 Mathematics Subject Classification.
54B20, 54C50.
Key words and phrases. Hyperspaces, finite graphs,
dimension, Whitney levels.
Glasnik Matematicki Home Page
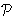 ,
there exist only finitely many X such that
,
there exist only finitely many X such that
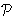 is homeomorphic to a
positive Whitney level for C(X).
is homeomorphic to a
positive Whitney level for C(X).