Glasnik Matematicki, Vol. 32, No.2 (1997), 213-215.
AN Lp INEQUALITY FOR
SELF-INVERSIVE POLYNOMIALS
N. K. Govil
Department of Mathematics, Auburn University, Auburn, AL 36849,
USA
Abstract. Let
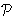
 denote the set of all polinomials p(z) of degree at
most n. Here we show that if p
denote the set of all polinomials p(z) of degree at
most n. Here we show that if p
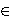
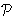
 and satisfies p(z) =
znp(1/z), then
and satisfies p(z) =
znp(1/z), then
n/2 ||p||δ
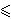 ||p'||δ
||p'||δ
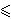 n Cδ1/δ ||p||δ,
n Cδ1/δ ||p||δ,
where Cδ = (2-δ
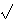 π
Γ(δ/2 + 1)) / (Γ(δ/2 + 1/2)).
The inequality on the right hand side is best possible and the equality
holds for polynomials p(z) =
a + bzn, |a| = |b|.
π
Γ(δ/2 + 1)) / (Γ(δ/2 + 1/2)).
The inequality on the right hand side is best possible and the equality
holds for polynomials p(z) =
a + bzn, |a| = |b|.
1991 Mathematics Subject Classification.
30A10, 30C10, 30E10.
Key words and phrases. Inequalities in the complex
domain, polynomials, approximation in the complex domain.
Glasnik Matematicki Home Page
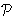
 denote the set of all polinomials p(z) of degree at
most n. Here we show that if p
denote the set of all polinomials p(z) of degree at
most n. Here we show that if p
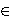
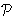
 and satisfies p(z) =
znp(1/z), then
and satisfies p(z) =
znp(1/z), then
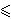 ||p'||δ
||p'||δ
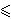 n Cδ1/δ ||p||δ,
n Cδ1/δ ||p||δ,
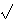 π
Γ(δ/2 + 1)) / (Γ(δ/2 + 1/2)).
The inequality on the right hand side is best possible and the equality
holds for polynomials p(z) =
a + bzn, |a| = |b|.
π
Γ(δ/2 + 1)) / (Γ(δ/2 + 1/2)).
The inequality on the right hand side is best possible and the equality
holds for polynomials p(z) =
a + bzn, |a| = |b|.