 the complexification of the Lie algebra of G0
and by K the complexification of K0.
Let T be a complex torus in K
and
the complexification of the Lie algebra of G0
and by K the complexification of K0.
Let T be a complex torus in K
and 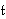 its Lie algebra. We can consider the categories
its Lie algebra. We can consider the categories
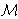 (
( ,K) and
,K) and
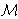 (
( ,T)
of Harish-Chandra modules for the pairs
(
,T)
of Harish-Chandra modules for the pairs
( ,K) and
(
,K) and
( ,T).
Clearly,
,T).
Clearly, 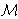 (
( ,T)
is a full subcategory of
,T)
is a full subcategory of
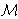 (
( )
and
)
and 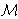 (
( ,K)
is a full subcategory of
,K)
is a full subcategory of
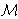 (
( ,T).
The natural forgetful functors have right adjoints
,T).
The natural forgetful functors have right adjoints
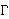 T,
T,
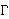 K and
K and
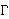 K,T.
These adjoints are called the Zuckerman functors.
Zuckerman functors are left exact and have finite right cohomological
dimension. Therefore, one can consider their right derived functors.
They are related by the obvious Grothendieck spectral sequence
K,T.
These adjoints are called the Zuckerman functors.
Zuckerman functors are left exact and have finite right cohomological
dimension. Therefore, one can consider their right derived functors.
They are related by the obvious Grothendieck spectral sequence
Rp
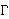 K,T
(Rq
K,T
(Rq
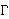 T(V))
T(V))
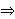 Rp+q
Rp+q
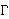 K(V),
K(V),
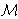 (
( ).
In this paper, this spectral sequence is investigated
in the case where V is the Verma module
M(
).
In this paper, this spectral sequence is investigated
in the case where V is the Verma module
M(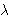 ).
The main result is the decomposition formula which strengthens
the Duflo-Vergne formula. This decomposition formula implies in
particular that the above spectral sequence degenerates.
).
The main result is the decomposition formula which strengthens
the Duflo-Vergne formula. This decomposition formula implies in
particular that the above spectral sequence degenerates.
The authors first show that a bounded complex (satisfying certain finiteness conditions) is isomorphic to the direct sum of its cohomologies if and only if its endomorphism algebra has maximal possible dimension. Next, they analyze the derived functors of the right adjoint to a forgetful functor. In the final section, they prove a decomposition formula for derived Zuckerman functors for tori, which then leads to their main results.