Glasnik Matematicki, Vol. 32, No.1 (1997), 99-124.
SHAPE AND UNIFORM PROPERTIES OF HYPERSPACES
OF NONCOMPACT SPACES
Takahisa Miyata and Jack Segal
Namazu College of Technology, 3600 OOka, Namazu 410, Japan
e-mail: miyata@cce.numazu-ct.ac.jp
Department of Mathematics, University of Washington, Seattle,
WA 98195, USA
e-mail: segal@math.washington.edu
Abstract. In this paper we study various shape and
uniform properties of hyperspaces of noncompact spaces. In the first
part we study shape properties of hyperspaces
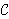 (X)
of nonempty compact subsets and symmetric products
(X)
of nonempty compact subsets and symmetric products
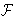
 (X)
(n
(X)
(n 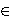
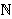
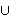 {
{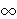 })
of noncompact spaces X in a systematic way, using approximate
resolutions in the sense of Mardesic and Watanabe. This enables
us to generalize the Kodama, Spiez and Watanabe results for the compact
case, and also the Dold and Thom result on the infinite
symmetric products of pointed CW-complexes. We also study approximate
resolutions of
})
of noncompact spaces X in a systematic way, using approximate
resolutions in the sense of Mardesic and Watanabe. This enables
us to generalize the Kodama, Spiez and Watanabe results for the compact
case, and also the Dold and Thom result on the infinite
symmetric products of pointed CW-complexes. We also study approximate
resolutions of
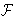
 (X)
for noncompact spaces X and give many applications. In the
second part we study the uniform contractibility property of
hyperspaces
(X)
for noncompact spaces X and give many applications. In the
second part we study the uniform contractibility property of
hyperspaces
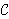 (X)
and 2X of nonempty closed subsets of noncompact
spaces X and discuss the uniform boundedness of X.
(X)
and 2X of nonempty closed subsets of noncompact
spaces X and discuss the uniform boundedness of X.
1991 Mathematics Subject Classification.
54B20, 54C56, 54E15, 55P55, 55Q07.
Key words and phrases. Hyperspace, symmetric product,
uniform space, approximate resolution, shape, uniform contractibility,
uniformly bounded, noncompact space.
Glasnik Matematicki Home Page
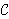 (X)
of nonempty compact subsets and symmetric products
(X)
of nonempty compact subsets and symmetric products
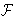
 (X)
(n
(X)
(n 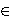
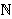
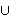 {
{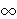 })
of noncompact spaces X in a systematic way, using approximate
resolutions in the sense of Mardesic and Watanabe. This enables
us to generalize the Kodama, Spiez and Watanabe results for the compact
case, and also the Dold and Thom result on the infinite
symmetric products of pointed CW-complexes. We also study approximate
resolutions of
})
of noncompact spaces X in a systematic way, using approximate
resolutions in the sense of Mardesic and Watanabe. This enables
us to generalize the Kodama, Spiez and Watanabe results for the compact
case, and also the Dold and Thom result on the infinite
symmetric products of pointed CW-complexes. We also study approximate
resolutions of
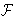
 (X)
for noncompact spaces X and give many applications. In the
second part we study the uniform contractibility property of
hyperspaces
(X)
for noncompact spaces X and give many applications. In the
second part we study the uniform contractibility property of
hyperspaces
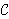 (X)
and 2X of nonempty closed subsets of noncompact
spaces X and discuss the uniform boundedness of X.
(X)
and 2X of nonempty closed subsets of noncompact
spaces X and discuss the uniform boundedness of X.