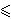n/2 M(p,1) and M(p,R)
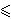(Rn+1)/2 M(p,1), R > 1.
Certain generalizations of these inequalities have been obtained.
The inequalities are sharp. Some applications are also considered.
Abstract. Let p(z) be a polynomial of
degree n and M(f,r) =
max|z|=r |f(z)|,
for an arbitrary entire function f(z). For
p(z) not vanishing in |z| < 1, we have
M(p',1)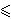
n/2 M(p,1) and M(p,R)
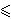(Rn+1)/2 M(p,1), R > 1.
Certain generalizations of these inequalities have been obtained.
The inequalities are sharp. Some applications are also considered.
1991 Mathematics Subject Classification. 30C10, 30A10.
Key words and phrases. Inequalities, generalization.