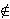 {
{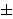 2,
2,
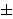 1
1
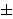 2i,
2i,
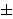 4i },
then there exists at least one quadruple with the property
D(z).
4i },
then there exists at least one quadruple with the property
D(z).
Abstract. A set of Gaussian integers is said to have the
property D(z) if the product of its any two distinct
elements increased by z is a square of a Gaussian integer.
In this paper it is proved that if a Gaussain integer z
is not representable as a difference of the squares of two
Gaussian integers, then there does not exist a quadruple with
the property D(z), but if z is representable
as a difference of two squares and if z
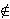 {
{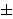 2,
2,
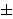 1
1
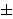 2i,
2i,
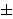 4i },
then there exists at least one quadruple with the property
D(z).
4i },
then there exists at least one quadruple with the property
D(z).
1991 Mathematics Subject Classification. 11D09.
Key words and phrases. Diophantine quadruple, property of Diophantus, Gaussian integers, Pell equation.