- M. Gardner, Mathematical games,
Scientific American 216 (1967), March 1967, p. 124; April 1967, p.119.
- J. H. van Lint, On a set of diophantine
equations, T. H.-Report 68 - WSK-03, Department of Mathematics,
Technological University Eindhoven, Eindhoven, 1968.
- A. Baker and H. Davenport,
The equations
3x2 - 2 = y2 and
8x2 - 7 = z2,
Quart. J. Math. Oxford Ser. (2) 20 (1969), 129-137.
- P. Kanagasabapathy and T. Ponnudurai, The
simultaneous Diophantine equations
y2 - 3x2 = -2 and
z2 - 8x2 = -7,
Quart. J. Math. Oxford Ser. (2) 26 (1975), 275-278.
- B. W. Jones, A variation on a problem of
Davenport and Diophantus, Quart. J. Math. Oxford Ser. (2)
27 (1976), 349-353.
- G. Sansone, Il sistema diofanteo
N + 1 = x2,
3N + 1 = y2,
8N + 1 = z2,
Ann. Mat. Pura Appl. (4) 111 (1976), 125-151.
- M. Gardner, Mathematical Magic Show,
Alfred Knopf, New York, 1977, pp. 210, 221-222.
- V. E. Hoggatt and G. E. Bergum, A problem of
Fermat and the Fibonacci sequence, Fibonacci Quart. 15
(1977), 323-330.
- G. Berzsenyi, Problem B-369,
Fibonacci Quart. 16 (1978), 565.
- P. E. Gibbs, Computer Bulletin 17
(1978), 16.
- C. M. Grinstead, On a method of solving a
class of Diophantine equations, Math. Comp. 32
(1978), 936-940.
- B. W. Jones, A second variation on a problem
of Diophantus and Davenport, Fibonacci Quart. 16
(1978), 155-165.
- C. Leach, Computer Bulletin 15 (1978), 13.
- J. Arkin, V. E. Hoggatt and E. G. Strauss,
On Euler's solution of a problem of Diophantus,
Fibonacci Quart. 17 (1979), 333-339.
- P. Heichelheim, The study of positive
integers
(a,b) such that ab + 1
is a square,
Fibonacci Quart. 17 (1979), 269-274.
- J. Arkin, V. E. Hoggatt and E. G. Strauss,
On Euler's solution of a problem of Diophantus II,
Fibonacci Quart. 18 (1980), 170-176.
- N. Thamotherampillai, The set of numbers
{1,2,7},
Bull. Calcutta Math. Soc. 72 (1980), 195-197.
- M. Veluppillai, The equations
z2 - 3y2 = -2 and
z2 - 6x2 = -5,
A Collection of Manuscripts Related to the Fibonacci sequence,
(V. E. Hoggatt, M. Bicknell-Johnson, eds.), The Fibonacci
Association, Santa Clara}, 1980, pp. 71-75.
- J. Morgado, Generalization of a result of
Hoggatt and Bergum on Fibonacci numbers, Portugaliae Math.
42 (1983-1984), 441-445.
- S. P. Mohanty and A. M. S. Ramasamy,
The simultaneous Diophantine equations
5y2 - 20 = x2 and
2y2 + 1 = z2, J. Number Theory
18 (1984), 356-359.
- E. Brown, Sets in which xy + k is
always a square,
Math. Comp. 45 (1985), 613-620.
- H. Gupta and K. Singh, On k-triad
sequences, Internat. J. Math. Math. Sci. 5 (1985), 799-804.
- S. P. Mohanty and A. M. S. Ramasamy,
The characteristic number of two simultaneous Pell's
equations and its application, Simon Stevin 59 (1985),
203-214.
- S. P. Mohanty and A. M. S. Ramasamy, On Pr,k sequences,
Fibonacci Quart. 23 (1985), 36-44.
- M. Nutt, Generalizations of Thamotherampillai's {1,2,7},
Bull. Calcuta Math. Soc. 78 (1986), 7-9.
- A. F. Horadam, Generalization of a result of
Morgado, Portugaliae Math. 44 (1987), 131-136.
- J. Morgado, A problem concerning the Fibonacci
numbers, Proceedings of the Second Meeting of Portuguese
Algebraist, Univ. Porto, Porto, 1987, pp. 77-88 (in Portuguese).
- D. X. Zheng, On the system of Diophantine
equations y2 - 2x2 = 1,
z2 - 5x2 = 4 and
y2 - 5x2 = 4,
z2 - 10x2 = 9,
Sichuan Daxue Xuebao 24 (1987), 25-29 (in Chinese).
- J. Arkin and G. E. Bergum,
More on the problem of Diophantus,
Application of Fibonacci Numbers, Vol. 2 (A. N. Philippou,
A. F. Horadam, G. E. Bergum, eds.), Kluwer, Dordrecht,
1988, pp. 177-181.
- G. Berzsenyi, Problems, puzzles, paradoxes, Consortium 25 (1988), 5.
- C. Long and G. E. Bergum, On a problem of
Diophantus, Application of Fibonacci Numbers, Vol 2 (A. N.
Philippou, A. F. Horadam, G. E. Bergum, eds.), Kluwer, Dordrecht, 1988,
pp. 183-191.
- A. G. Shannon, Fibonacci numbers and
Diophantine quadruples: Generalizations of results of Morgado and
Horadam, Portugaliae Math. 45 (1988), 165-169.
- V. K. Mootha and G. Berzsenyi,
Characterization and extendibility of
Pt-sets, Fibonacci Quart. 27
(1989), 287-288.
- H. Altindis, Generalization of the set
{1,2,5}, Istanbul Univ. Fen Fak. Mat. Derg. 49
(1990), 1-5.
- J. H. Chen, Common solutions of the Pell
equations x2 - 2y2 = 1
and
y2 - Dz2 = 4,
J. Wuhan Univ. Natur. Sci. Ed. (1990), 8-12.
- A. Dujella, A problem of Diophantus and
Fibonacci numbers, Matematika (Zagreb) 19 (3) (1990),
45-52 (in Croatian).
- D. Zagier, Elliptische Kurven: Fortschritte
und Anwendungen, Jahresber. Deutsch. Math.-Verein 92
(1990), 58-76.
- G. Berzsenyi, Adventures among
Pt-sets, Quantum 1 (4) (1991), 57.
- J. Morgado, Note on a Shannon's theorem
concerning the Fibonacci numbers and Diophantine quadruples,
Portugaliae Math. 48 (1991), 429-439.
- D. M. Bloom, Problem 10238, Amer. Math. Monthly
99 (1992), 674.
- J. Roberts, Lure of the Integers, The
Mathematical Association of America, 1992, pp. 31-35.
- D. X. Zheng, On the system of Diophantine
equations
a2x2 -
a1y2 =
a2 - a1,
a3y2
- a2z2 =
a3 - a2,
Sichuan Daxue Xuebao 29 (1992), 348-351 (in Chinese).
- J. Arkin, D. C. Arney, F. R. Giordano,
R. A. Kolb and G. E. Bergum,
An extension of an old classical Diophantine problem,
Application of Fibonacci Numbers, Vol. 5 (G. E. Bergum,
A. N. Philippou, A. F. Horadam, eds.), Kluwer, Dordrecht, 1993,
pp. 45-48.
- A. Dujella, Generalization of a problem of
Diophantus, Acta Arith. 65 (1993), 15-27.
- H. Altindis,
On P2j
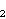 sets, Bull. Calcuta Math. Soc. 86 (1994), 305-306.
sets, Bull. Calcuta Math. Soc. 86 (1994), 305-306.
- G. Berzsenyi, Problem 4/14, Mathematics and Informatics Quarterly 5 (1995), 103-105.
- R. Drnovsek, Solution of Problem 10238, Amer.
Math. Monthly 102 (1995), 275-276.
- A. Dujella, Diophantine quadruples for squares
of Fibonacci and Lucas numbers, Portugaliae Math. 52
(1995), 305-318.
- V. K. Mootha, On the set of numbers
{14,22,30,42,90},
Acta Arith. 71 (1995), 259-263.
- J. Morgado, Note on the Chebyshev polynomials
and applications to the Fibonacci numbers, Portugaliae Math.
52 (1995), 363-378.
- A. M. S. Ramasamy, A remarkable sequence,
Banyan Mathematical Journal 2 (1995), 69-76.
- Gh. Udrea, A problem of Diophantos-Fermat and
Chebyshev polynomials of the second kind, Portugaliae Math.
52 (1995), 301-304.
- Z. Y. Chen, The Diophantine system of
equations 5x2 - 3y2 = 2,
16y2 - 5z2 = 11,
J. Central China Normal Univ. Natur. Sci. 30 (1996),
381-384 (in Chinese).
- M. N. Deshpande and G. E. Bergum, Interesting
arrays associated with Fibonacci sequences, Applications of
Fibonacci Numbers, Vol. 6 (G. E. Bergum, A. N. Philippou, A. F.
Horadam, eds.), Kluwer, Dordrecht, 1996, pp. 85-92.
- A. Dujella, Generalized Fibonacci numbers and
the problem of Diophantus, Fibonacci Quart. 34
(1996), 164-175.
- A. Dujella, Some polynomial formulas for
Diophantine quadruples, Grazer Math. Ber. 328
(1996), 25-30.
- A. Dujella, Generalization of the Problem of
Diophantus and Davenport, Dissertation, University of Zagreb,
1996 (in Croatian).
- S. T. Thakar, The role of "T" and "S" of
IMTS, Mathematics and Informatics Quarterly 6
(1996), 23-26.
- Gh. Udrea, A note on the sequence
(Wn) of A. F. Horadam,
Portugaliae Math. 53 (1996), 143-155.
- Z. Y. Chen, Upper bounds for positive integer
solutions of the indeterminate equations
x2 - 7y2 = 2,
z2 - 32y2 = -23,
J. Central China Normal Univ. Natur. Sci. 31
(1997), 253-256 (in Chinese).
- M. N. Deshpande, Problem 10622, Amer. Math. Monthly 104 (1997), 870.
- A. Dujella, On Diophantine quintuples,
Acta Arith. 81 (1997), 69-79.
- A. Dujella, The problem of Diophantus and
Davenport for Gaussian integers, Glas. Mat. Ser. III 32
(1997), 1-10.
- A. Dujella, The problem of the extension of a
parametric family of Diophantine triples,
Publ. Math. Debrecen 51 (1997), 311-322.
- A. Dujella, The problem of Diophantus and
Davenport, Math. Commun. 2 (1997), 153-160.
- M. N. Deshpande, One property of triangular
numbers, Portugaliae Math. 55 (1998), 381-383.
- A. Dujella, On the exceptional set in the
problem of Diophantus and Davenport, Application of Fibonacci
Numbers, Vol. 7 (G. E. Bergum, A. N. Philippou, A. F. Horadam, eds.),
Kluwer, Dordrecht, 1998, pp. 69-76.
- A. Dujella, A problem of Diophantus and Pell
numbers, Application of Fibonacci Numbers, Vol. 7 (G. E. Bergum,
A. N. Philippou, A. F. Horadam, eds.), Kluwer, Dordrecht, 1998, pp.
61-68.
- A. Dujella, A problem of Diophantus and
Dickson's conjecture, Number Theory, Diophantine, Computational
and Algebraic Aspects (K. Gyory, A. Petho, V. T. Sos, eds.),
Walter de Gruyter, Berlin, 1998, pp. 147-156.
- A. Dujella, Some estimates of the number of
Diophantine quadruples, Publ. Math. Debrecen 53
(1998), 177-189.
- A. Dujella, Complete solution of a family of
simultaneous Pellian equations, Acta Math. Inform. Univ.
Ostraviensis 6 (1998), 59-67.
- A. Dujella, Diophantine quadruples and
quintuples modulo 4,
Notes Number Theory Discrete Math. 4 (1998), 160-164.
- A. Dujella and A. Petho, A generalization of
a theorem of Baker and Davenport, Quart. J. Math. Oxford Ser. (2),
49 (1998), 291-306.
- K. S. Kedlaya, When is
(xy+1)(yz+1)(zx+1) a square?,
Math. Mag. 71 (1998), 61-63.
- K. S. Kedlaya, Solving constrained Pell
equations, Math. Comp. 67 (1998), 833-842.
- Z. Y. Chen, The system of Diophantine
equations
(m + 2)x2 - my2 = 2,
(4m + 4)y2 -
(m + 2)z2 = 3m + 2,
J. Central China Normal Univ. Natur. Sci. 33 (1999), 1-5.
- A. Dujella, A proof of the Hoggatt-Bergum
conjecture, Proc. Amer. Math. Soc. 127 (1999), 1999-2005.
- A. Dujella, An extension of an old problem of
Diophantus and Euler, Fibonacci Quart. 37 (1999), 312-314.
- Z. Franco, Solution of Problem 10622, Amer. Math.
Monthly 106 (1999), 868.
- P. Gibbs, A generalised Stern-Brocot tree from
regular Diophantine quadruples, XXX Mathematics Archive math.NT/9903035.
- E. Herrmann, A. Petho and H. G. Zimmer, On
Fermat's quadruple equations, Abh. Math. Sem. Univ. Hamburg
69 (1999), 283-291.
- L. Jones, A polynomial approach to a
Diophantine problem, Math. Mag. 72 (1999), 52-55.
- A. Petho, Algebraische Algorithmen,
Vieweg, Braunschweig, 1999, pp. 106-115.
- E. W. Weisstein, CRC Concise Encyclopedia of
Mathematics, Chapman & Hall / CRC, Boca Raton, 1999, p. 759.
- H. Widmer, Solution of Problem 10622, Amer. Math.
Monthly 106 (1999),
867-868.
- M. N. Deshpande, An interesting
conjecture, The Mathematical Gazette 84 (2000), 296-298.
- A. Dujella, Diophantine triples and
construction of high-rank elliptic curves over
 with three
non-trivial 2-torsion points, Rocky Mountain J. Math.
30 (2000), 157-164.
with three
non-trivial 2-torsion points, Rocky Mountain J. Math.
30 (2000), 157-164.
- A. Dujella, A note on Diophantine
quintuples, Algebraic Number Theory and Diophantine Analysis
(F. Halter-Koch, R. F. Tichy, eds.), Walter de Gruyter, Berlin, 2000,
pp. 123-127.
- A. Dujella, A parametric family of elliptic
curves, Acta Arith. 94 (2000), 87-101.
- A. Dujella, Irregular Diophantine
m-tuples and high-rank elliptic curves, Proc. Japan Acad.
Ser. A Math. Sci. 76 (2000), 66-67.
- A. Dujella and A. Petho, Integer points on a
family of elliptic curves, Publ. Math. Debrecen 56 (2000),
321-335.
- O. Kihel, On the extendibility of the set {1,2,5},
Fibonacci Quart. 38 (2000), 464-466.
- Gh. Udrea, A problem of Diophantus-Fermat and
Chebyshev polynomials of the first kind, Rev. Roumaine Math. Pures
Appl. 45 (2000), 531-535.
- E. Assaf and S. Gueron, Characterization of
regular Diophantine quadruples, Elem. Math. 56 (2001),
71-81.
- M. N. Deshpande and E. Brown, Diophantine
triplets and the Pell sequence, Fibonacci Quart. 39
(2001), 242-249.
- A. Dujella, An absolute bound for the size of
Diophantine m-tuples, J. Number Theory 89
(2001), 126-150.
- A. Dujella, Diophantine m-tuples
and elliptic curves, J. Theor. Nombres Bordeaux 13
(2001), 111-124.
- P. Gibbs, Diophantine quadruples and Cayley's
hyperdeterminant, XXX Mathematics Archive math.NT/0107203
- K. Gyarmati, On a problem of Diophantus,
Acta Arith. 97 (2001), 53-65.
- K. Gyarmati, Powers, powerful and powerfree
numbers in sumsets and multiplicative structures, Master Thesis, Eotvos University, Budapest, 2001 (in Hungarian).
- A. Kihel and O. Kihel, Sets in which the
product of any k elements increased by t is a
kth-power, Fibonacci Quart. 39 (2001), 98-100.
- A. Kihel and O. Kihel, On the intersection
and the extendability of
Pt sets, Far East J.
Math. Sci. 3 (2001), 637-643.
- A. F. Beardon and M. N. Deshpande,
Diophantine triples, The Mathematical Gazette 86
(2002), 258-260.
- M. N. Deshpande, One interesting family of
diophantine triplets, Internat. J. Math. Ed. Sci. Tech.
33 (2002), 253-256.
- M. N. Deshpande, A problem in number
theory, Resonance 7(7) (2002), 89-91.
- M. N. Deshpande and A. Dujella, An
interesting property of a reccurence related to the Fibonacci
sequence, Fibonacci Quart. 40 (2002), 157-160.
- A. Dujella, On the size of Diophantine
m-tuples, Math. Proc. Cambridge Philos. Soc.
132 (2002), 23-33.
- A. Dujella, An extension of an old problem of
Diophantus and Euler. II, Fibonacci Quart.
40 (2002), 118-123.
- A. Dujella, C. Fuchs and R. F. Tichy,
Diophantine m-tuples for linear polynomials,
Period. Math. Hungar. 45 (2002), 21-33.
- C. Fuchs, Quantitative finiteness results
for Diophantine equations, Dissertation, TU Graz, 2002.
- K. Gyarmati, A. Sarkozy and C. L. Stewart,
On shifted products which are powers, Mathematika
49 (2002), 227-230.
- M. J. Jacobson, Jr. and H. C. Williams,
Modular arithmetic on elements of small norm in quadratic
fields, Des. Codes and Cryptogr. 27 (2002), 93-110.
- Y. Bugeaud and A. Dujella, On a problem
of Diophantus for higher powers, Math. Proc. Cambridge
Philos. Soc. 135 (2003), 1-10.
- M. N. Deshpande, Families of Diophantine triplets,
Bulletin of the Marathwada Mathematical Society 4
(2003), 19-21.
- A. Dujella and C. Fuchs, A polynomial
variant of a problem of Diophantus and Euler,
Rocky Mountain J. Math. 33 (2003), 797-811.
- F. S. Abu Muriefah and A. Al- Rashed,
On the exendibility of the Diophantine triple {1,5,c},
Internat. J. Math. Math. Sci. 33 (2004), 1737-1746.
- F. S. Abu Muriefah and A. Al- Rashed,
Some Diophantine quadruples in the ring
Z[√-2], Math. Commun.
9 (2004), 1-8.
- J. Almeida and A. Machiavelo,
Jose Morgado, Bulletin of International Center for
Mathematics 17 (2004), 24-27.
- J. Almeida and A. Machiavelo,
Jose Morgado: in memoriam, Boletim da SPM
50 (2004), 1-18.
- Y. Bugeaud,
On the Diophantine equation
(xk-1)(yk-1) =
(zk-1),
Indag. Math. 15 (2004), 21-28.
- Y. Bugeaud and K. Gyarmati, On generalizations
of a problem of Diophantus, Illinois J. Math.
48 (2004), 1105-1115.
- A. Dujella, There are only finitely many
Diophantine quintuples, J. Reine Angew. Math.
566 (2004), 183-214.
- A. Dujella, Bounds for the size of sets with
the property D(n), Glas. Mat. Ser. III
39 (2004), 199-205.
- A. Dujella, Diophantine
quadruples and Fibonacci numbers,
Bulletin of Kerala Mathematical Association
1 (2004), 133-147.
- A. Dujella and C. Fuchs,
Complete solution of the polynomial version of a problem of
Diophantus, J. Number Theory 106 (2004), 326-344.
- Z. Franusic,
Diophantine quadruples in the ring
Z[√2], Math. Commun.
9 (2004), 141-148.
- R. K. Guy, Unsolved Problems in Number
Theory, 3rd edition, Springer-Verlag, New York, 2004,
Section D29, p. 310.
- D. Saraswathy, A Study on Sets of Numbers with Diophantine Property,
M.Phil. Dissertation, Department of Mathematics, Pondicherry University,
Pondicherry, 2004.
- M. Waldschmidt,
Open Diophantine problems, Moscow Math. J.
4 (2004), 245-305.
- R. Dietmann, C. Elsholtz, K. Gyarmati and M. Simonovits,
Shifted products that are coprime pure powers,
J. Combin. Theory Ser. A 111 (2005), 24-36.
- A. Dujella and C. Fuchs,
Complete solution of a problem of Diophantus and Euler,
J. London Math. Soc. 71 (2005), 33-52.
- A. Dujella and F. Luca,
Diophantine m-tuples for primes,
Int. Math. Res. Not. 47 (2005), 2913-2940.
- A. Dujella and A. M. S. Ramasamy,
Fibonacci numbers and sets with the property
D(4),
Bull. Belg. Math. Soc. Simon Stevin 12 (2005), 401-412.
- A. Filipin, Non-extendibility of
D(-1)-triples of the form {1,10,c}, Internat. J. Math. Math. Sci. 35 (2005) 2217-2226.
- Z. Franusic, Diophantine Quadruples in
Quadratic Fields, Dissertation, University of Zagreb,
2005 (in Croatian).
- C. Fuchs,
Upper Bounds for the Solutions of Diophantine Problems, Habilitation Thesis, TU Graz, 2005.
- K. Gyarmati,
A polynomial extension of a problem of Diophantus,
Publ. Math. Debrecen 66 (2005), 389-405.
- F. Luca, On shifted products
which are powers, Glas. Mat. Ser. III 40 (2005), 13-20.
- F. S. Abu Muriefah and A. Al- Rashed,
On the simultaneous Diophantine equations
y2 - 5x2 = 4 and
z2 - 442x2 = 441,
Arab. J. Sci. Eng. Sect. A Sci. 31 (2006) 207-211.
- A. Dujella, C. Fuchs and P. G. Walsh,
Diophantine m-tuples for linear polynomials. II. Equal
degrees, J. Number Theory 120 (2006), 213-228.
- A. Filipin,
Systems of Pellian Equations and the Problem of Extension of Some Diophantine Triples,
Dissertation, University of Zagreb, 2006 (in Croatian).
- Y. Fujita, The unique representation d = 4k(k2 - 1)
in D(4)-quadruples {k-2, k+2, 4k, d},
Math. Commun. 11 (2006), 69-81.
- Y. Fujita, The non-extensibility of D(4k)-triples
{1, 4k(k-1), 4k2+1} with |k| prime, Glas. Mat. Ser. III
41 (2006), 205-216.
- P. Gibbs, Some rational Diophantine
sextuples, Glas. Mat. Ser. III 41 (2006), 195-203.
- P.-C. Hu, C.-C. Yang, Value Distribution Theory Related to Number Theory,
Birkhäuser, Basel, 2006, pp. 335-336.
- Y. Li, An upper bound for the positive integer
solutions of the system of Diophantine equations
7x2-5y2=2,
24y2-7z2=17,
J. Chongqing Norm. Univ. Nat. Sci. Ed. 23 (2006), 33-35. (in Chinese).
- A. Silvester, Fast and Unconditional Principal Ideal Testing,
Master's thesis, University of Calgary, 2006.
- Y. Bugeaud, A. Dujella, M. Mignotte,
On the family of Diophantine triples {k - 1, k + 1, 16k^3 - 4k},
Glasgow Math. J. 49 (2007), 333-344.
- A. Dujella, On Mordell-Weil groups of
elliptic curves induced by Diophantine triples, Glas. Mat. Ser. III
42 (2007), 3-18.
- A. Dujella, A. Filipin and C. Fuchs,
Effective solution of the D(-1)-quadruple conjecture,
Acta Arith. 128 (2007), 319-338.
- A. Dujella and F. Luca, On a problem of
Diophantus with polynomials,
Rocky Mountain J. Math. 37 (2007), 131-157.
- A. Filipin, Extensions of some parametric families of
D(16)-triples, Internat. J. Math. Math. Sci.
2007 (2007), Article ID 63739, 12 pages
- Y. Fujita, The extensibility of
D(-1)-triples {1,b,c}, Publ. Math. Debrecen 70 (2007), 103-117.
- Y. Fujita, The D(1)-extensions of D(-1)-triples
{1, 2, c} and integer points on the attached elliptic curves, Acta Arith.
128 (2007), 349-375.
- K. Gyarmati and C. L. Stewart, On powers in
shifted products, Glas. Mat. Ser. III 42 (2007), 273-279.
- T. Liqun, On the property P-1, Integers 7 (2007), #A47
- K. Kaygisiz and H. Senay, Constructions of some new nonextandable
Pk sets, International Mathematical Forum 2 (2007), 2869-2874.
- A. M. S. Ramasamy, Sets and sequences
linked with a question of Diophantus, Bulletin of Kerala Mathematics Association
4 (2007), 109-125.
- M. N. Deshpande, Diophantine triples from recurrence relations,
preprint.
- A. Dujella, On the number of Diophantine
m-tuples
, Ramanujan J. 15 (2008), 37-46.
- A. Dujella, C. Fuchs and F. Luca,
A polynomial variant of a problem of Diophantus for pure powers,
Int. J. Number Theory 4 (2008), 57-71.
- A. Dujella and V. Petricevic,
Strong Diophantine triples, Experiment. Math. 17 (2008), 83-89.
- A. Filipin, On the size of sets in which xy + 4
is always a square, Rocky Mountain J. Math. 39 (2009), 1195-1224.
- A. Filipin, There does not exist a D(4)-sextuple,
J. Number Theory 128 (2008), 1555-1565.
- A. Filipin and Y. Fujita, Any polynomial D(4)-quadruple
is regular, Math. Commun. 13 (2008), 45-55.
- Z. Franusic, Diophantine quadruples in
Z[√(4k+3)], Ramanujan J. 17 (2008), 77-88.
- Z. Franusic, A Diophantine problem in
Z[(1+√d)/2], Studia Sci. Math. Hungar.
46 (2009), 103-112.
- Y. Fujita, The extensibility of Diophantine
pairs {k-1, k+1}, J. Number Theory 128 (2008), 322-353.
- Y. Fujita, The Hoggatt-Bergum conjecture on D(-1)-triples
{F2k+1, F2k+3, F2k+5}
and integer points on the attached elliptic curves, Rocky Mountain J. Math. 39 (2009), 1907-1932.
- C. L. Stewart, On sets of integers whose
shifted products are powers, J. Combin. Theory Ser. A 115 (2008), 662-673.
- G. Campbell and E. H. Goins, Heron triangles,
Diophantine problems and elliptic curves, preprint.
- Y. Fujita, Any Diophantine quintuple contains
a regular Diophantine quadruple, J. Number Theory 129 (2009), 1678-1697.
- Y. Fujita, The number of Diophantine quintuples,
Glas. Mat. Ser. III 45 (2010), 15-29.
- A. J. MacLeod, Square Eulerian quadruples,
Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 20 (2016), 1-7.
- D. S. Nagaraj and P. Shastri, On the determination of
Diophantine triples, in: Number Theory and Applications (S. D. Adhikari,
B. Ramakrishnan, eds.), Hindustan Book Agency, 2009, pp. 139-148.
- R. Tamura, Non-extendibility of
D(-1)-triples {1,b,c}, preprint.
- C. Fuchs, F. Luca and L. Szalay, Diophantine triples
with values in binary recurrences, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5)
7 (2008), 579-608.
- F. Luca and L. Szalay, Fibonacci Diophantine triples,
Glas. Mat. Ser. III 43 (2008), 253-264.
- K. Kaygisiz, H. Senay and N. Bircan,
Construction of some new nonextended Pk sets, preprint.
- A. Dujella, Conjectures and results on the size and number of Diophantine tuples,
Diophantine Analysis and Related Fields (DARF 2007/2008),
AIP Conf. Proc. 976 (T. Komatsu, ed.), Amer. Inst. Phys., Melville, NY, 2008, pp. 58-61.
- Y. Fujita, Diophantine quadruples containing some triples
and the number of Diophantine quintuples,
Diophantine Analysis and Related Fields (DARF 2007/2008),
AIP Conf. Proc. 976 (T. Komatsu, ed.), Amer. Inst. Phys., Melville, NY, 2008, pp. 90-95.
- Z. Franusic, On the extensibility of Diophantine triples
{k-1, k+1, 4k}
for Gaussian integers, Glas. Mat. Ser. III 43 (2008), 265-291.
- J.-M. de Koninck and A. Mercier, 1001 Problems in Classical Number Theory,
American Mathematical Society, Providence, 2007, pp. 284-285.
- F. Najman, Compact representation of quadratic integers and integer
points on some elliptic curves, Rocky Mountain J. Math. 40 (2010), 1979-2002.
- A. Filipin, An irregular D(4)-quadruple cannot be extended to a quintuple,
Acta Arith. 136 (2009), 167-176.
- F. Najman, Integer points on two families of elliptic curves,
Publ. Math. Debrecen 75 (2009), 401-418.
- A. Dujella, Rational Diophantine sextuples with mixed signs,
Proc. Japan Acad. Ser. A Math. Sci. 85 (2009), 27-30.
- Bo He and A. Togbé, On the family of Diophantine triples
{k+1, 4k, 9k+3}, Period. Math. Hungar. 58 (2009), 59-70.
- Bo He and A. Togbé, On a family of Diophantine triples
{k, A2k+2A, (A+1)2k+2(A+1)}
with two parameters,
Acta Math. Hungar. 124 (2009), 99-113.
- A. Filipin, There are only finitely many D(4)-quintuples,
Rocky Mountain J. Math. 41 (2011), 1847-1860.
- A. Filipin and A. Togbé, On the family of Diophantine triples
{k+2, 4k, 9k+6}, Acta Math. Acad. Paedagog. Nyhazi. 25 (2009), 145-153.
- F. Luca and L. Szalay, Lucas Diophantine triples,
Integers 9 (2009), #A35, 441-457.
- S.-C. Yang, On the solutions of the Pell Equations
x2-7y2=2,
32y2-z2=23,
Journal of Tianzhong 22 (2007). (in Chinese).
- W. D. Banks, F. Luca and L. Szalay,
A variant on the notion of a diophantine s-tuple,
Glasgow Math. J. 51 (2009), 83-89.
- G. Martin and S. Sitar,
Erdös-Turán with a moving target, equidistribution of roots of
reducible quadratics, and Diophantine quadruples, Mathematika 57 (2011), 1-29.
- A. Dujella and A. Jurasic,
On the size of sets in a
polynomial variant of a problem of Diophantus, Int. J. Number Theory 6 (2010), 1449-1471.
- H. Balasunderam,
The set of numbers {1, 5, 10}, J. Natn. Sci. Coun. Sri Lanka
6 (1978), 23-26.
- P. Gibbs, Adjugates of Diophantine quadruples,
Integers 10 (2010), 201-209.
- A. Dujella and I. Soldo,
Diophantine quadruples in Z[√-2],
An. Stiint. Univ. "Ovidius" Constanta Ser. Mat. 18 (2010), 81-98.
- J.-M. de Koninck, Those Fascinating Numbers,
American Mathematical Society, Providence, 2009, p. 120.
- A. Filipin, On the polynomial parametric
family of the sets with the property D(-1;1), Bol. Soc. Mat. Mexicana 16 (2010), 1-8.
- Y. Fujita, Extensions of the D(∓k2)-triples
{k2, k2 ± 1, 4k2 ± 1},
Period. Math. Hungar. 59 (2009), 21-33.
- A. Filipin, Bo He and A. Togbé, On a family of two-parametric D(4)-triples,
Glas. Mat. Ser. III 47 (2012), 31-51.
- A. Filipin, Bo He and A. Togbé, On the D(4)-triple
{ F2k, F2k+6, 4F2k+4 },
Fibonacci Quart. 48 (2010), 219-227.
- A. Filipin and Y. Fujita, The number of D(-1)-quadruples, Math. Commun.
15 (2010), 387-391.
- H. Hemme, Mathematik zum Frühstück.
89 mathematische Rätsel mit ausführlichen Lösungen,
Vandenhoeck & Ruprecht, Göttingen, 1990, p. 40, 130.
- B. Sriraman and H. Adrian, The existential void in learning: Juxtaposing mathematics
and literature, in: Interdisciplinarity, Creativity, and Learning
(B. Sriraman, V. Freiman, N. Lirette-Pitre, eds.), Age Publishing, 2009, pp. 13-29.
- T. Koshy, Fibonacci and Lucas Numbers with Applications,
Wiley, New York, 2001, pp. 93-95.
- J. Aguirre, A. Dujella and J. C. Peral,
On the rank of elliptic curves coming from rational Diophantine triples, Rocky Mountain J. Math.
42 (2012), 1759-1776.
- B. He and A. Togbé, On a family of Diophantine triples
{k, A2k+2A, (A+1)2k+2(A+1)}
with two parameters II,
Period. Math. Hungar. 64 (2012), 1-10.
- Z. Cerin and G. M. Gianella, On Diophantine triples from Pell and Pell-Lucas numbers,
Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 143 (2009), 83-94.
- Z. Y. Chen, The system of Diophantine equations
9x2 - 7y2 = 2,
32y2 - 9z2 = 23,
J. Central China Normal Univ. Natur. Sci. 30 (1996),
24-28 (in Chinese).
- Z. S. Zheng, On an upper bound for the positive integer solutions
of the system of Diophantine equations
11x2 - 9y2 = 2,
40y2 - 11z2 = 29,
Math. Practice Theory 38 (2008), 210-214 (in Chinese).
- Y. Li, An upper bound for the positive integer
solutions of the system of Diophantine equations
6x2-4y2=2,
20y2-6z2=14,
J. Chongqing Norm. Univ. Nat. Sci. Ed. 24 (2009), 19-21 (in Chinese).
- A. Filipin and Y. Fujita,
The D(-k2)-triple {1,k2+1,k2+4}
with k prime, Glas. Mat. Ser. III 46 (2011), 311-323.
- M. N. Deshpande, Problem 94.C, The Mathematical Gazette 94 (2010), 159.
- Z. Cerin and G. M. Gianella, On D(-4) and D(8) triples
from Pell and Pell-Lucas numbers,
Rend. Circ. Mat. Palermo (2) Suppl. 81 (2009), 73-83.
- Y. Fujita and A. Togbé, The extension of the D(-k2)-pair
{k2, k2 + 1}, Period. Math. Hungar. 65 (2012), 75-81.
- G. N. Özcan, Diophantine Quadruples and Generalized Bivariate Polynomial
Sequences, M. Sc. Thesis, Selcuk University, Konya, 2009 (in Turkish).
- A. Nalli and G. N. Özcan, Generalized bivariate polynomials
and Diophantine quadruples, preprint.
- H. Altindis, Characterization and extendability of Pk
sets for k ≡ 3(4), Gazi University Journal of Science 23 (2010), 295-297.
- A. Jurasic,
Diophantine m-tuples for quadratic polynomials, Glas. Mat. Ser. III
46 (2011), 283-309.
- B. He and A. Togbé,
On the D(-1)-triple {1,k2+1,k2+2k+2}
and its unique D(1)-extension, J. Number Theory 131 (2011), 120-137.
- R. Esdahl-Schou,
Diophantine tuple, Student project, University of Aarhus, 2009.
- F. Najman, Compact Representation of Quadratic Integers and Integer Points
on Elliptic Curves, Dissertation, University of Zagreb, 2010 (in Croatian).
- A. Jurasic, Polinomial Variants of a Problem of Diophantus,
Dissertation, University of Zagreb, 2010 (in Croatian).
- Z. Franusic, On the extension of the Diophantine pair {1,3} in
Z[√d], J. Integer Seq. 13 (2010), Article 10.9.6
- P. Corvaja and U. Zannier, An abcd Theorem over function fields
and applications, Bull. Soc. Math. France 139 (2011), 437-454.
- A. Filipin, Y. Fujita and M. Mignotte,
The non-extendibility of some parametric families of D(-1)-triples, Q. J. Math.
63 (2012), 605-621.
- A. Bérczes, A. Dujella, L. Hajdu and F. Luca,
On the size of sets whose elements have perfect power n-shifted products,
Publ. Math. Debrecen 79 (2011), 325-339.
- L. Bapoungue, The system of Diophantine equations
7z2 - 20y2 = -52 and
3z2 -20x2 = -68, Internat. J. Algebra, Number theory and Applications,
1 (2009), 1-11.
- A. Dujella and A. Jurasic,
Some Diophantine triples and quadruples for quadratic polynomials, J. Comb. Number Theory
3(2) (2011), 123-141.
- S. Prugsapitak and V. Laohakosol,
Some families of Diophantine quadruples, ScienceAsia 37 (2011), 152-159.
- N. C. Bonciocat, M. Cipu and M. Mignotte,
On D(-1)-quadruples, Publ. Mat. 56 (2012), 279-304.
- A. Filipin and Y. Fujita,
The number of Diophantine quintuples II, Publ. Math. Debrecen 82 (2013), 293-308.
- W. Narkiewicz,
Teoria liczb w tworczosci Eulera, Wiadom. Mat. 43 (2007), 87-98.
- A. Filipin and Y. Fujita,
The relative upper bound for the third element in a D(-1)-quadruple, Math. Commun.
17 (2012), 13-19.
- A. Dujella and C. Fuchs, On a problem of Diophantus for rationals,
J. Number Theory 132 (2012), 2075-2083.
- Z. Cerin, G. M. Gianella, Matrices with rows in Euler triples from Pell and
Pell-Lucas numbers, JP J. Algebra Number Theory Appl. 21 (2011), 117-132.
- Z. Cerin, Determinants and permanents of matrices from Fibonacci and Lucas numbers,
Pioneer Journal of Algebra, Number Theory and its Applications 1 (2011), 9-22.
- Z. Franusic and D. Kreso, Nonextensibility of the pair {1,3} to a Diophantine quintuple in
Z[√-2], J. Comb. Number Theory 3(3) (2011), 1-15.
- M. N. Deshpande, Problem B-1073, Fibonacci Quart.
48 (2010), 278.
- B. P. Beasley, Solution of Problem B-1073, Fibonacci Quart.
49 (2011), 276-277.
- Z. Cerin, Squares from D(-4) and D(20) triples,
Advances in Pure Mathematics 1 (2011), 286-294.
- W. Narkiewicz, Rational Number Theory in the 20th Century. From PNT to FLT,
Springer, London, 2012, Section 6.6.4, pp. 351-352.
- A. Nowicki, Podroze po Imperium Liczb, 03 Liczby Kwadratowe,
Wydawnictwo OWSIiZ, Olsztyn, 2009, Chapter 6, pp. 87-97.
- A. M. S. Ramasamy and D. Saraswathy,
A non-extendable Diophantine quadruple arising from a triple of Lucas numbers, Involve
5 (2012), 257-271.
- Y. Fujita and A. Togbé,
Uniqueness of the extension of the D(4k2)-triple
{k2 - 4, k2, 4k2 - 4},
Notes Number Theory Discrete Math. 17(4) (2011), 42-49.
- L. Szalay and V. Ziegler,
On an S-unit variant of Diophantine m-tuples,
Publ. Math. Debrecen 83 (2013), 97-121.
- Z. Cerin,
Pencils of Euler triples, I,
Sarajevo J. Math. 8 (2012), 15-31.
- Z. Cerin,
On extended Euler quadruples, Atti Semin. Mat. Fis. Univ. Modena Reggio Emilia
58 (2011), 101-120.
- Y. Zhang,
Diophantine triples and extendibility of {1,2,5} and {1,5,10},
Master Thesis, Central Michigan University, 2011.
- W. Rich,
Regular Diophantine m-tuples and their extensions,
PhD Thesis, Central Michigan University, 2012.
- Z. Cerin,
Pencils of Euler triples, II,
Sarajevo J. Math. 8 (2012), 179-192.
- Lj. Jukic Matic,
Non-existence of certain Diophantine quadruples in rings of integers of pure cubic fields,
Proc. Japan Acad. Ser. A Math. Sci. 88 (2012), 163-167.
- A. Ipek,
On algebraic properties of the generalized Chebyshev polynomials,
Transylv. J. Math. Mech. 2 (2010), 59-66.
- Lj. Bacic and A. Filipin,
On the family of D(4)-triples {k - 2, k + 2, 4k3 - 4k},
Bull. Belg. Math. Soc. Simon Stevin 20 (2013), 777-787.
- Lj. Bacic and A. Filipin,
On the extendibility of D(4)-pair {k - 2, k + 2},
J. Comb. Number Theory 5 (2013), 181-197.
- A. Filipin, Y. Fujita and A. Togb´e,
The extendibility of Diophantine pairs I: the general case, Glas. Mat. Ser. III
49 (2014), 25-36.
- I. Soldo,
On the existence of Diophantine quadruples in Z[√-2], Miskolc Math. Notes
14 (2013), 265-277.
- I. Soldo,
On the extensibility of D(-1)-triples {1, b, c} in the ring
Z[√-t], t > 0, Studia Sci. Math. Hungar. 50 (2013), 296-330.
- H. Lao, On the number of Diophantine m-tuples,
Adv. Math. (China) 39 (2010), 277-282.
- A. Dujella and J. C. Peral,
High rank elliptic curves with torsion Z/2Z × Z/4Z
induced by Diophantine triples,
LMS J. Comput. Math. 17 (2014), 282-288.
- M. Alp, N. Irmak and L. Szalay, Balancing diophantine triples,
Acta Univ. Sapientiae Math. 4 (2012), 11-19.
- K. R. Matthews, J. P. Robertson and J. White,
On a Diophantine equation of Andrej Dujella, Glas. Mat. Ser. III 48 (2013), 265-289.
- F. Luca and L. Szalay,
On the Fibonacci distances of ab, ac and bc,
Ann. Math. Inform. 41 (2013), 137-163.
- A. Dujella and N. Saradha,
Diophantine m-tuples with elements in arithmetic progressions, Indag. Math. (N.S.)
25 (2014), 131-136.
- A. Dujella and M. Mikic,
On the torsion group of elliptic curves induced by D(4)-triples,
An. Stiint. Univ. "Ovidius" Constanta Ser. Mat. 22 (2014), 79-90.
- Z. Franusic,
Diophantine quadruples in the ring of integers of Q( 3√2),
Miskolc Math. Notes 14 (2013), 893-903.
- Lj. Jukic Matic,
On D(w)-quadruples in the rings of integers of certain pure number fields,
Glas. Mat. Ser. III 49 (2014), 37-46.
- C. Elsholtz, A. Filipin and Y. Fujita,
On Diophantine quintuples and D(-1)-quadruples,
Monatsh. Math. 175 (2014), 227-239.
- L. Szalay and V. Ziegler, S-Diophantine quadruples with two primes
congruent 3 modulo 4, Integers 13 (2013), #A80.
- A. Srinivasan, On the prime divisors of elements of a D(-1)
quadruple, Glas. Mat. Ser. III 49 (2014), 275-285.
- Lj. Bacic and A. Filipin,
The extendibility of D(4)-pairs, Math. Commun. 18 (2013), 447-456.
- Z. Cerin,
Squares in Euler triples from Fibonacci and Lucas numbers,
Cubo 15 (2013), 79-88.
- M. Mikic, On the Mordell-Weil group of elliptic curves
induced by the families of Diophantine triples, Rocky Mountain J. Math. 45 (2015), 1565-1589.
- J. McLean, Pk-sets,
Mathematical Spectrum 24 (1992), 78-79.
- W. Wu and B. He, On Diophantine quintuple conjecture,
Proc. Japan Acad. A Math. Sci. 90 (2014), 84-86.
- I. Soldo,
D(-1)-triples of the form {1, b, c} in the ring
Z[√-t], t > 0, Bull. Malays. Math. Sci. Soc. (2) 39 (2016), 1201-1224.
- G. Srividhya, Diophantine quadruples for Fibonacci numbers
with property D(1),
Indian Journal of Mathematics and Mathematical Sciences 5 (2009), 57-59.
- M. A. Gopalan and V. Pandichelvi,
On the extendibility of the Diophantine triple involving Jacobsthal numbers
(J2n-1, J2n+1 - 3,
2J2n + J2n-1 + J2n+1 - 3),
International Journal of Mathematics & Applications 2 (2009), 1-3.
- V. Pandichelvi, Construction of the Diophantine triple involving polygonal numbers,
Impact J. Sci. Tech. 5 (2011), 7-11.
- M. A. Gopalan and G. Srividhya, Diophantine quadruples for Fibonacci
and Lucas numbers with property D(4),
Diophantus J. Math. 1 (2012), 15-18.
- M. A. Gopalan and G. Srividhya, Some non-extendable P-5 sets,
Diophantus J. Math. 1 (2012), 19-22.
- M. A. Gopalan and G. Srividhya, Two special Diophantine triples,
Diophantus J. Math. 1 (2012), 23-27.
- M. A. Gopalan, V. Sangeetha and M. Somanath,
Construction of the Diophantine triple involving polygonal numbers,
Sch. J. Eng. Tech. 2 (2014), 19-22.
- B. Peker, A. Dujella and S. Cenberci,
The non-extensibility of D(-2k+1)-triples
{1, k2, k2+2k-1},
Miskolc Math. Notes 16 (2015), 385-390.
- F. Luca and V. Ziegler, A note on the number of S-Diophantine quadruples,
Commun. Math. 22 (2014), 49-55.
- K. S. Bhanu and M. N. Deshpande,
Interesting dates,
Mathematics in School 44 (2015), 37.
- L. Szalay and V. Ziegler, S-Diophantine quadruples with
S = {2, q}, Int. J. Number Theory 11 (2015), 849-868.
- K. Meena, S. Vidhyalakshmi, M. A. Gopalan, G. Akila and R. Presenna,
Formation of special Diophantine quadruples with property
D(6kpq)2, The International Journal of Science & Technoledge
2 (2014), 11-14.
- M. A. Gopalan, S. Vidhyalakshmi and S. Mallika,
Some special non-extendable Diophantine triples,
Sch. J. Eng. Tech. 2 (2014), 159-160.
- C. A. Gomez Ruiz and F. Luca,
Tribonacci Diophantine quadruples, Glas. Mat. Ser. III 50 (2015), 17-24.
- M. A. Gopalan, S. Vidhyalakshmi, E. Premalatha and K. Presenna,
On the extendibility of 2-tuple to 4-tuple with property D(4),
Bulletin of Mathematical Sciences & Applications 3 (2014), 100-104.
- Lj. Bacic and A. Filipin,
A note on the number of D(4)-quintuples,
Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 18 (2014), 7-13.
- Z. Franusic and I. Soldo,
The problem of Diophantus for integers of Q(√-3),
Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 18 (2014), 15-25.
- S. Vidhyalakshmi, M. A. Gopalan and K. Lakshmi,
Gaussian - Diophantine quadruples with property D(1),
IOSR Journal of Mathematics 10 (2014), 12-14.
- M. Cipu and Y. Fujita,
Bounds for Diophantine quintuples,
Glas. Mat. Ser. III 50 (2015), 25-34.
- A. Filipin, Y. Fujita and A. Togbé,
The extendibility of Diophantine pairs II: examples,
J. Number Theory 145 (2014), 604-631.
- A. Filipin,
The extendibility of D(4)-pair
{F2k, 5F2k},
Fibonacci Quart. 53 (2015), 124-129.
- A. Srinivasan,
D(-1)-quadruples and products of two primes, Glas. Mat. Ser. III 50 (2015), 261-268.
- K. Meena, S. Vidhyalakshmi, M. A. Gopalan and R. Presenna,
Special Dio-triples, JP J. Algebra Number Theory Appl. 31 (2014), 13-25.
- Z. Zhang,
The Diophantine equation
(axk-1)(byk-1) =
abzk-1, J. Number Theory 136 (2014), 252-260.
- I. Soldo,
Some Diophantine Problems over the Imaginary Quadratic Fields,
Dissertation, University of Zagreb,
2012 (in Croatian).
- Lj. Bacic,
Sets in which xy + 4 is always a square and problem of the extensibility
of some parametric Diophantine triples, Dissertation, University of Zagreb,
2014 (in Croatian).
- M. Mikic,
Mordell-Weil Groups and Isogenies of the Families of Elliptic Curves,
Dissertation, University of Zagreb,
2014 (in Croatian).
- K. Aktas, On the solutions of congruence equations in the Gaussian integers
ring and biquadratic residues, Master Thesis, Selcuk University, 2008 (in Turkish).
- L. Bapoungue,
The system of Diophantine equations
(u-1)x2 - 4uy2 = -12u-8 and
(u+2)x2 - 4uz2 = -12u+8
, Sciencia Acta Xaveriana 4 (2013), 1-20.
- M. Alp, N. Irmak and L. Szalay,
Reduced diophantine quadruples with the binary recurrence
Gn = AGn-1-Gn-2,
An. Stiint. Univ. "Ovidius" Constanta Ser. Mat. 23 (2015), 23-31.
- N. Irmak and L. Szalay,
Diophantine triples and reduced quadruples with the Lucas sequence of recurrence
un = Aun-1 - un-2,
Glas. Mat. Ser. III 49 (2014), 303-312.
- M. Alp, N. Irmak and L. Szalay, Balancing Diophantine triples with distance 1,
Period. Math. Hungar. 71 (2015), 1-10.
- M. Cipu, Further remarks on Diophantine quintuples, Acta Arith. 168 (2015),
201-219.
- D. J. Platt and T. S. Trudgian,
Diophantine quintuples containing triples of the first kind, Period. Math. Hungar. 72 (2016), 235-242.
- T. S. Trudgian,
Bounds on the number of Diophantine quintuples,
J. Number Theory 157 (2015), 233-249.
- A. Bérczes, F. Luca, I. Pink and V. Ziegler,
Finiteness results for Diophantine triples with repdigit values, Acta Arith. 172 (2016), 133-148.
- A. Filipin and A. Jurasic,
On the size of Diophantine m-tuples for linear polynomials,
Miskolc Math. Notes 17 (2016), 861-876.
- M. Cipu, A. Filipin and Y. Fujita,
Bounds for Diophantine quintuples II, Publ. Math. Debrecen 88 (2016), 59-78.
- F. Izadi and F. Khoshnam,
On elliptic curves via Heron triangles and Diophantine triples,
J. Math. Ext. 8 (2014), 17-26.
- Z. Cerin and G. M. Gianella,
On Jones S(E)-triples and S(E)-quadruples in rings,
Rend. Circ. Mat. Palermo (2) Suppl. No. 83 (2011), 95-109.
- Z. Cerin and G. M. Gianella,
Square in Euler triples from Pell and Pell-Lucas numbers,
Rend. Circ. Mat. Palermo (2) Suppl. No. 84 (2012), 187-194.
- C. A. Gomez Ruiz and F. Luca,
Diophantine quadruples in the sequence of shifted Tribonacci numbers,
Publ. Math. Debrecen 86 (2015), 473-491.
- A. Bérczes, A. Dujella, L. Hajdu and Sz. Tengely,
Finiteness results for F-Diophantine sets, Monatsh. Math. 180 (2016), 469-484.
- A. Dujella, M. Kazalicki, M. Mikic and M. Szikszai,
There are infinitely many rational Diophantine sextuples,
Int. Math. Res. Not. IMRN 2017 (2) (2017), 490-508.
- A. W. Dudek,
On the number of divisors of n2 - 1,
Bull. Aust. Math. Soc. 93 (2016), 194-198.
- M. Cipu and T. Trudgian,
Searching for Diophantine quintuples, Acta Arith. 173 (2016), 365-382.
- A. Bayad, A. Filipin and A. Togbé,
Extension of a parametric family of Diophantine triples in Gaussian integers,
Acta Math. Hungar. 148 (2016), 312-327.
- C. Fuchs, C. Hutle, N. Irmak, F. Luca and L. Szalay,
Only finitely many Tribonacci Diophantine triples exist, Math. Slovaca 67 (2017), 853-862.
- Y. Fujita and T. Miyazaki,
The regularity of Diophantine quadruples, Trans. Amer. Math. Soc. 370 (2018), 3803-3831.
- K. Lapkova,
Explicit upper bound for an average number of divisors of quadratic polynomials,
Arch. Math. (Basel) 106 (2016), 247-256.
- F. Bencherif, N. Benyahia Tani, S. Bouroubi, O. Kihel and Z. Yahi,
Integer partitions into Diophantine pairs,
Quaest. Math. 40 (2017), 435-442.
- Bo He, A. Pinter, A. Togbé and S. Yang,
Another generalization of a theorem of Baker and Davenport,
J. Number Theory 182 (2018), 325-343.
- Y. Zhang and G. Grossman,
Diophantine triples and extendibility of {1,2,5} and {1,5,10},
Fibonacci Quart. 52 (2014), 212-215.
- C. A. Gómez Ruiz,
Números Tribonacci, S-unidades y triplas diofánticas,
Rev. Integr. Temas Mat. 33 (2015), 121-133.
- C. Fuchs, C. Hutle, F. Luca and L. Szalay,
Diophantine triples and k-generalized Fibonacci sequences,
Bull. Malays. Math. Sci. Soc. (2) 41 (2018), 1449-1465.
- Y. Zhang and G. Grossman,
On Diophantine triples and quadruples,
Notes Number Theory Discrete Math. 21(4) (2015), 6-16.
- A. Dujella, M. Jukic Bokun and I. Soldo,
On the torsion group of elliptic curves induced by
Diophantine triples over quadratic fields,
Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 111 (2017), 1177-1185.
- A. M. S. Ramasamy,
Diophantine quadruples and near-diophantine quintuples
from P3,k sequences, Asian-Eur. J. Math. 10 (2017), 1750010 (13 pp)
- M. Bliznac and A. Filipin,
An upper bound for the number of Diophantine quintuples, Bull. Aust. Math. Soc.
94 (2016), 384-394.
- A. Dujella,
What is ... a Diophantine m-tuple?, Notices Amer. Math. Soc. 63 (2016), 772-774.
- Lj. Bacic Djurackovic and A. Filipin,
The extendibility of D(4)-pairs {F2k, F2k+6}
and {P2k, P2k+4},
Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 20 (2016), 27-35.
- A. Dujella and M. Kazalicki,
More on Diophantine sextuples, in
Number Theory - Diophantine problems, uniform distribution and applications,
Festschrift in honour of Robert F. Tichy's 60th birthday
(C. Elsholtz, P. Grabner, Eds.), Springer-Verlag, Berlin, 2017, pp. 227-235.
- J. Harrington and L. Jones,
A problem of Diophantus modulo a prime, Irish Math. Soc. Bull. 77 (2016), 45-49.
- F. Luca and A. O. Munagi,
Diophantine triples with values in the sequences of Fibonacci and Lucas numbers,
Glas. Mat. Ser. III 52 (2017), 23-43.
- A. Bayad, A. Dossavi-Yovo, A. Filipin and A. Togbé,
On the extensibility of the D(4)-triple {k - 2, k + 2, 4k} over Gaussian integers,
Notes Number Theory Discrete Math. 23 (2017), 1-26.
- A. Dossavi-Yovo, Bo He and A. Togbé,
The extensibility of the D(±k)-triple {k ∓ 1, k, 4k ∓ 1},
Afrika Mat. 28 (2017), 563-574.
- B. He, F. Luca and A. Togbé,
Diophantine triples of Fibonacci numbers,
Acta Arith. 175 (2016) , 57-70.
- A. Dujella and M. Kazalicki,
Diophantine m-tuples in finite fields and modular forms,
Res. Number Theory 7 (2021), Article number 3, (24pp)
- P. E. Gibbs,
Regular rational Diophantine sextuples, preprint.
- P. E. Gibbs,
A survey of rational Diophantine sextuples of low height, preprint.
- B. He, A. Togbé and V. Ziegler,
There is no Diophantine quintuple, Trans. Amer. Math. Soc. 371 (2019), 6665-6709.
- N. Adžaga and A. Filipin,
On the extension of D(-8k2)-pair {8k2, 8k2 + 1},
Mosc. Math. J. 17 (2017), 165-174.
- D. M. Burton,
Elementary Number Theory,
7th edition, McGraw-Hill, New York, 2011, p. 33.
- T. Cai,
The Book of Numbers,
World Scientific, Singapore, 2017, pp. 206-209.
- N. Irmak and M. Alp,
Pellans sequence and its Diophantine triples,
Publ. Inst. Math. 100 (2016), 259-269.
- M. Cipu, Y. Fujita and M. Mignotte,
Two-parameter families of uniquely extendable Diophantine triples,
Sci. China Math. 61 (2018), 421-438.
- S. Bujačić and A. Filipin,
Linear forms in logarithms,
in Diophantine Analysis: Course Notes from a Summer School (J. Steuding, Ed.),
Birkhäuser, Basel, 2016, pp. 1-59.
- I. Chajda,
Diofantovské n-tice,
Matematika - fyzika - informatika 26 (2017), 1-6.
- Ö. Özer,
On the some particular sets,
Kirklareli University Journal of Engineering and Science 2 (2016) 99-108.
- M. Bliznac Trebješanin, A. Filipin and A. Jurasić,
On the polynomial quadruples with the property D(-1;1),
Tokyo J. Math. 41 (2018), 527-540.
- N. Adžaga, A. Dujella, D. Kreso and P. Tadić,
Triples which are D(n)-sets for several n's, J. Number Theory 184 (2018), 330-341.
- M. Bliznac Trebješanin and A. Filipin,
Nonexistence of D(4)-quintuples, J. Number Theory 194 (2019), 170-217.
- K. Lapkova,
Explicit upper bound for the average number of divisors of irreducible quadratic polynomials,
Monatsh. Math. 186 (2018), 663-673.
- A. Filipin,
The extension of some D(4)-pairs, Notes Number Theory Discrete Math. 23 (2017), 126-135.
- A. Filipin and A. Jurasic,
A polynomial variant of a problem of Diophantus and its consequences,
Glas. Mat. Ser. III 54 (2019), 21-52.
- F. Luca and Y. Fujita,
On Diophantine quadruples of Fibonacci numbers, Glas. Mat. Ser. III 52 (2017), 221-234.
- A. Dujella, M. Jukić Bokun and I. Soldo,
A Pellian equation with primes and applications to D(-1)-quadruples,
Bull. Malays. Math. Sci. Soc 42 (2019), 2915-2926.
- J. B. Lee, J. Park,
Some conditions on the form of third element from Diophantine pairs and its application,
J. Korean Math. Soc. 55 (2018), 425-445.
- M. Sadek, N. El Sissi,
On large F-Diophantine sets, Monatsh. Math. 186 (2018), 703-710.
- A. M. S. Ramasamy,
Diophantine quadruples of numbers whose elements are in proportion,
Tamkang J. Math. 48 (2017), 241-249.
- M. Cipu, Y. Fujita and T. Miyazaki,
On the number of extensions of a Diophantine triple,
Int. J. Number Theory 14 (2018), 899-917.
- K. Lapkova,
On the average number of divisors of reducible quadratic polynomials,
J. Number Theory 180 (2017), 710-729.
- M. Stoll,
Diagonal genus 5 curves, elliptic curves over Q(t),
and rational diophantine quintuples, Acta Arith. 190 (2019), 239-261.
- S. Cenberci and B. Peker,
On some P2 sets,
Pure Mathematical Sciences 6 (2017), 61-66.
- B. Peker and S. Cenberci,
On the equations y2 - 10x2 = 9 and
z2 - 17x2 = 16,
International Mathematical Forum 12 (2017), 715-720.
- G. Nyul,
Diofantoszi számhalmazok,
Középiskolai Matematikai és Fizikai Lapok 67 (2017), 391-395.
- C. Fuchs, C. Hutle and F. Luca,
Diophantine triples in linear recurrence sequences of Pisot type,
Res. Number Theory 4 (2018), Paper No. 29, 22 pp.
- M. Krizek, F. Luca and L. Somer,
Aritmeticke vlastnosti Fibonacciovych cisel,
Pokroky matematiky, fyziky a astronomie 50 (2005), 127-140.
- A. Dujella and J. C. Peral,
Elliptic curves induced by Diophantine triples,
Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 113 (2019), 791-806.
- G. K. Gözeri,
On Pell, Pell-Lucas, and balancing numbers,
J. Inequal. Appl. 2018 (2018), Paper No. 3, 16 pp.
- M. Bliznac Trebješanin,
Diophantine D(4)-m-tuples and Related Problems,
Dissertation, University of Zagreb, 2018 (in Croatian).
- A. Dujella, I. Gusic, V. Petricevic and P. Tadic,
Strong Eulerian triples, Glas. Mat. Ser. III 53 (2018), 33-42.
- Y. Bugeaud, Linear Forms in Logarithms and Applications,
IRMA Lectures in Mathematics and Theoretical Physics Vol. 28,
European Mathematical Society, 2018, Sections 3.8 and 5.4.
- P. Gibbs, Diophantine quintuples over quadratic rings, preprint, 2018.
- Y. Fujita and T. Miyazaki, Extendabilities of a Diophantine triple to quadruples,
RIMS Kokyuroku 2014 (2017), 111-123. (in Japanese)
- T. Trudgian, A wishlist for Diophantine quintuples,
RIMS Kokyuroku 2014 (2017), 124-131.
- M. Somanath, J. Kannan and K. Raja, Construction of a parametric family of
Diophantine triples in integers,
Indian Journal in Number Theory (2018), 1-6.
- S. E. Rihane, M. O. Hernane and A. Togbé,
On the D(4)-Diophantine triples of Fibonacci numbers,
Fibonacci Quart. 56 (2018), 63-74.
- N. Adzaga, A. Dujella, D. Kreso and P. Tadic,
On Diophantine m-tuples and D(n)-sets,
RIMS Kokyuroku 2092 (2018), 130-137.
- B. He, K. Pu, R. Shen and A. Togbé,
A note on the regularity of the Diophantine pair {k, 4k ± 4},
J. Theor. Nombres Bordeaux 30 (2018), 879-892.
- M. Cipu, A. Filipin and Y. Fujita,
An infinite two-parameter family of Diophantine triples,
Bull. Malays. Math. Sci. Soc. 43 (2020), 481-498.
- N. Adzaga, Diophantine m-tuples in the Rings of Integers,
Dissertation, University of Zagreb, 2018 (in Croatian).
- O. Cira, Diophantine triples of superior order,
ISREIE Conference, 7th Edition, Mathematics & Computer Science (2018), 35-54.
- Y. Fujita and F. Luca, There are no Diophantine quadruples of Fibonacci numbers,
Acta Arith. 185 (2018), 19-38.
- N. Adzaga,
On the size of Diophantine m-tuples in imaginary quadratic number rings,
Bull. Math. Sci. 11(1) (2021) 1950020 (10 pages).
- V. Ziegler,
On the existence of S-Diophantine quadruples, Glas. Mat. Ser. III 54 (2019), 279-319.
- C. A. Gomez Ruiz and F. Luca,
Diophantine quadruples with values in k-generalized Fibonacci numbers,
Math. Slovaca 68 (2018), 939-949.
- M. Cipu, A. Dujella and Y. Fujita,
Diophantine triples with largest two elements in common,
Period. Math. Hungar. 82 (2021), 56-68.
- R. Becker and M. Ram Murty,
Diophantine m-tuples with the property D(n),
Glas. Mat. Ser. III 54 (2019), 65-75.
- M. Cipu, A. Filipin and Y. Fujita,
Diophantine pairs that induce certain Diophantine triples, J. Number Theory 210 (2020), 433-475.
- J. Harrington and L. Jones,
A modification of a problem of Diophantus, Math. Slovaca 68 (2018), 1343-1352.
- M. Krizek, L. Somer and A. Solcova,
Kouzlo cisel. Od velkych objevu k aplikacim, Academia, Praha, 2018, pp. 241-242.
- K. Gueth,
Diophantine triples in a Lucas-Lehmer sequence, Ann. Math. Inform. 49 (2018), 85-100.
- A. Dujella and V. Petricevic,
Diophantine quadruples with the properties D(n1) and D(n2),
Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 114 (2020), Article 21 (9 pages).
- M. Cipu,
A new approach to the study of D(-1)-quadruples,
RIMS Kokyuroku 2092 (2018), 122-129.
- N. Mani and S. Rubinstein-Salzedo,
Diophantine tuples over Zp, Acta Arith. 197 (2021), 331-351.
- A. Dujella, M. Kazalicki and V. Petricevic,
Rational Diophantine sextuples with square denominators,
J. Number Theory 205 (2019), 340-346.
- T. Miyazaki,
Coincidence between two binary recurrent sequences of polynomials arising from Diophantine triples,
Tokyo J. Math. 42 (2019), 611-619.
- M. Jukic Bokun and I. Soldo,
On the extensibility of D(-1)-pairs containing Fermat primes,
Acta Math. Hungar. 159 (2019), 89-108.
- A. Dujella, M. Kazalicki and V. Petricevic,
Rational Diophantine sextuples containing two regular quadruples and one regular quintuple,
Acta Mathematica Spalatensia 1 (2021), 19-27.
- A. E. Rihane, M. O. Hernane and A. Togbe,
On Diophantine triples of Pell numbers, Colloq. Math. 156 (2019), 273-285.
- A. Dujella and V. Petricevic,
On the largest element in D(n)-quadruples, Indag. Math. (N.S.) 30 (2019) 1079-1086.
- O. Ozer,
Some results on especial Diophantine sets with size 3,
Journal of Advanced Mathematics and Mathematics Educaton 2 (2019), 1-11.
- Z. Franusic and B. Jadrijevic,
D(n)-quadruples in the ring of integers of Q(√2,√3), Math. Slovaca
69 (2019), 1263-1278.
- F. Luca,
Diophantine S-quadruples with two primes which are twin, Acta Math. Hungar.
159 (2019), 589-602.
- A. H. Phulpoto, I. Ahmed, A. Hameed, I. Soomro, R. Muhammed, I. A. Jokhio,
R. chohan, A. N. Kalhoro, S. N. Phulpoto and A. D. Jumani,
Diophantine Quadruple with D(9) property,
IJCSNS International Journal of Computer Science and Network Security 19 (2019), 245-248.
- J. Park and J. B. Lee,
Some family of Diophantine pairs with Fibonacci numbers,
Indian J. Pure Appl. Math. 19 (2019), 367-384.
- N. Adzaga, A. Filipin and Z. Franusic,
On the extensions of the Diophantine triples in Gaussian integers,
Monatsh. Math. 197 (2022), 535-563.
- A. N. Kalhoro, I. Soomro, A. H. Junejo, I. A. Memon, R. Muhammed, I. A. Jokhio,
R. chohan and A. D. Jumani,
Diophantine Quadruple with D(100) property,
IJCSNS International Journal of Computer Science and Network Security 19 (2019), 236-238.
- A. H. Phulpoto, I. Ahmed, I. Soomro, A. Hameed, R. Muhammed, I. A. Jokhio,
R. Chohan, A. N. Kalhoro, S. N. Phulpoto and A. D. Jumani,
Some polynomial formula of the Diophantine Quadruple with D(n) property,
IJCSNS International Journal of Computer Science and Network Security 19 (2019), 249-251.
- M. Bliznac Trebješanin,
Extension of a Diophantine triple with the property D(4),
Acta Math. Hungar. 163 (2021), 213-246.
- S. Earp-Lynch,
Diophantine Triples and Linear Forms in Logarithms,
Master Thesis, Brock University, 2019.
- B. Earp-Lynch,
Linear Forms in Logarithms and Fibonacci Numbers,
Master Thesis, Brock University, 2019.
- Ö. Özer and Z. C. Sahin,
On some particular regular Diophantine 3-tuples,
Math. Nat. Sci. 3 (2018), 29-38.
- A. M. Güloglu and M. Ram Murty,
The Paley graph conjecture and Diophantine m-tuples,
J. Combin. Theory Ser. A 170 (2020), Article 105155.
- C. Fuchs and S. Heintze,
Another S-unit variant of Diophantine tuples,
Proc. Amer. Math. Soc. 149 (2021), 27-35.
- A. Dujella, Number Theory, Skolska knjiga, Zagreb, 2019, (in Croatian),
Sections 14.6, 16.7.
- A. Dujella and J. C. Peral,
Construction of high rank elliptic curves, J. Geom. Anal. 31 (2021), 6698-6724.
- N. Adzaga, A. Filipin and Y. Fujita,
The extension of the D(-k)-pair {k, k + 1} to a quadruple,
Period. Math. Hungar. 85 (2022), 148-163.
- A. Dujella, M. Paganin and M. Sadek,
Strong rational Diophantine D(q)-triples, Indag. Math. (N.S.) 31 (2020), 505-511.
- A. Dujella and V. Petricevic,
Doubly regular Diophantine quadruples,
Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 114 (2020), Article 189, (8pp)
- S. Bouroubi and A. Debbache,
Thue’s equation as a tool to solve two different problems, Acta Comment. Univ. Tartu. Math.
25 (2021), 153-156.
- G. Drazic and M. Kazalicki,
Rational D(q) quadruples, Indag. Math. (N.S.) 33 (2022), 440-449.
- S. G. Rayaguru, G. K. Panda and A. Togbé,
On Diophantine, pronic and triangular triples of balancing numbers,
Math. Commun. 25 (2020), 137-155.
- O. Aytekin Celik,
Some Ps Diophantine triples for especial s integer,
Journal of Advanced Mathematics and Mathematics Educaton 3 (2020), 1-9.
- S. Gupta,
D(-1) tuples in imaginary quadratic fields, Acta Math. Hungar. 164 (2021), 556-569.
- A. M. S. Ramasamy,
Polynomials yielding quadruples with property D(k),
J. of Ramanujan Society of Mathematics and Mathematical Sciences 7 (2019), 53-64.
- Y. Fujita,
The number of irregular Diophantine quadruples for a fixed Diophantine pair or triple,
Contemp. Math. 768 (2021), 105-118.
- A. Dujella and J. C. Peral,
High rank elliptic curves induced by rational Diophantine triples,
Glas. Mat. Ser. III 55 (2020), 237-252.
- A. Dujella and M. Mikic,
Rank zero elliptic curves induced by rational Diophantine triples,
Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 24 (2020), 29-37.
- C. Fuchsa and S. Heintze,
A polynomial variant of Diophantine triples in linear recurrences,
Period. Math. Hungar. 86 (2023), 289-299.
- A. Chung and R. Raval,
There is no Diophantine quintuple,
Leicester Undergraduate Mathematical Journal 2 (2020).
- A. Filipin and Z. Franusic,
Diophantine Sets, Lecture notes, University of Zagreb, 2020 (in Croatian).
- B. Earp-Lynch, S. Earp-Lynch and O. Kihel,
On certain D(9) and D(64) Diophantine triples,
Acta Math. Hungar. 162 (2020), 483-517.
- J. Park,
Relation between Diophantine triple and elliptic curve,
J. Chungcheong Math. Soc. 33 (2020), 227-236.
- A. Filipin and A. Jurasic,
Diophantine quadruples in Z[i][X], Period. Math. Hungar. 82 (2021), 198-212.
- J. Park,
Integer points on the elliptic curves induced by Diophantine triples,
Commun. Korean Math. Soc. 35 (2020), 745-757.
- A. Dujella, Z. Franusic and V. Petricevic,
Formulas for Diophantine quintuples containing two pairs
of conjugates in some quadratic fields, Period. Math. Hungar. 85 (2022), 303-311.
- J. Park,
The extendibility of Diophantine pairs with property D(-1),
Korean J. Math. 28 (2020), 539-554.
- N. C. Bonciocat, M. Cipu and M. Mignotte,
There is no Diophantine D(-1)-quadruple, J. London Math. Soc. 105 (2022), 63-99.
- K. N. Adedji, A. Filipin and A. Togbé,
The problem of the extension of D(4)-triple {1, b, c},
Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 26 (2022), 21-43.
- V. Ziegler,
Finding all S-Diophantine quadruples for a fixed set of primes S,
Monatsh. Math. 196 (2021), 617-641.
- A. Dujella, M. Kazalicki and V. Petricevic,
D(n)-quintuples with square elements,
Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 115 (2021), Article 172, (10pp)
- A. Filipin, M. Jukic Bokun and I. Soldo,
On D(-1)-triples {1, 4p2 + 1, 1 - p} in the ring
Z[√-p] with a prime p, Period. Math. Hungar. 85 (2022), 292-302.
- N. Adzaga, A. Filipin and A. Jurasic,
The extensibility of the Diophantine triple {2, b, c},
An. Stiint. Univ. "Ovidius" Constanta Ser. Mat. 29 (2021), 5-24.
- M. Jukic Bokun and I. Soldo,
Pellian equations of special type,
Math. Slovaca 71 (2021), 1599-1607.
- K. N. Adedji, A. Filipin and A. Togbé,
On the family of Diophantine pairs {P2k, 2P2k+2},
Fibonacci Quart. 60 (2022), 25-39.
- N. Irmak,
Generalized Tribonacci Diophantine quadruples, Math. Rep. (Bucur.) 23 (2021), 465-474.
- M. Kazalicki and B. Naskrecki (with an appendix by L. Lasic),
Diophantine triples and K3 surfaces, J. Number Theory 236 (2022), 41-70.
- S. Saranya and V. Pandichelvi,
Classification of an exquisite diophantine 4-tuples bestow with an order,
Malaya J. Mat. 9 (2021), 612-615.
- S. Ibrahimpasic, Diophantine m-tuples,
Master Thesis, University of Bihac, 2014 (in Bosnian).
- B. Milosevic, Chord-Tangent Group Law on a Cubic Curves.
Mordell’s Finite Generation Theorem, Master Thesis, University of Belgrade, 2020 (in Serbian).
- A. Dujella, Number Theory, Skolska knjiga, Zagreb, 2021,
Sections 14.6, 16.7.
- K. N. Adedji, B. He, A. Pinter and A. Togbe,
On the Diophantine pair {a, 3a},
J. Number Theory 227 (2021), 330-351.
- A. E. Youmbai, M. Uludag and D. Behloul,
Elliptic curve involving subfamilies of rank at least 5 over Q(t) or Q(t,k),
Hacet. J. Math. Stat. 50 (2021), 721-731.
- A. Dujella and G. Soydan,
On elliptic curves induced by rational Diophantine quadruples, Proc. Japan Acad. Ser. A Math. Sci.
98 (2022), 1-6.
- G. Drazic,
Rational D(q)-quintuples,
Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 116 (2022), Article 9, (18pp).
- Z. Franusic,
Diophantine quintuples containing two pairs of conjugates in some quadratic fields,
Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 26 (2022), 45-53.
- G. Drazic,
A parametrization of rational D(q)-triples,
Mat. Bilten 45 (2021), 7-16.
- J. Park,
Diophantine triple with Fibonacci numbers and elliptic curve,
Commun. Korean Math. Soc. 36 (2021), 401-411.
- J. Park,
The extendibility of Diophantine pairs with Fibonacci numbers and some conditions,
J. Chungcheong Math. Soc. 34 (2021), 209-219.
- P. Gibbs, Diophantine quadruples and ideal solutions of the Prouhet-Tarry-Escott
problem of size four, preprint, 2021.
- B. Grechuk,
Landscape of 21st Century Mathematics. Selected Advances, 2001–2020, Springer, Cham, 2021,
Section 1.4, pp. 17-18.
- G. Drazic, Rational D(q)-m-tuples,
Dissertation, University of Zagreb, 2021 (in Croatian).
- A. D. Denton, A holiday brain teaser,
The Sunday Times, 4th August 1957, 18th August 1957.
- M. Cipu, A. Dujella and Y. Fujita,
Extensions of a Diophantine triple by adjoining smaller elements,
Mediterr. J. Math. 19 (2022), Article 187, (20pp)
- K. N. Adedji, A. Filipin and A. Togbé,
The extension of the D(-k)-triple {1, k, k+1},
Acta Math. Hungar. 166 (2022), 407-422.
- T. Hammonds, S. Kim, S. J. Miller, A. Nigam, K. Onghai, D. Saikia and L. M. Sharma,
k-Diophantine m-tuples in finite fields,
Int. J. Number Theory 19 (2023), 891-912.
- A. B. Dixit, S. Kim and M. Ram Murty,
Generalized Diophantine m-tuples,
Proc. Amer. Math. Soc. 150 (2022), 1455-1465.
- S. E. Rihane, F.Luca and A. Togbé,
There are no Diophantine quadruples of Pell numbers,
Int. J. Number Theory 18 (2022), 27-45.
- Y. Fujita and I. Soldo,
On D(-1)-tuples in the ring Z[√-k] with k > 0,
Publ. Math. Debrecen 100 (2022), 49-67.
- M. N. Deshpande, Diophantine triplets revisited,
The Mathematical Gazette 90 (2006), 445-448.
- C. Saranya and B. Achya, Diophantine triplets involving square pyramidal numbers,
Advances and Applications in Mathematical Sciences 21 (2022), 1541-1547.
- M. Bliznac Trebješanin,
D(4)-triples with two largest elements in common,
Math. Slovaca 73 (2023), 343-352.
- M. Cipu, Y. Fujita and M. Mignotte,
The unique extensions of two parametric families of Diophantine triples,
RIMS Kokyuroku 2203 (2021), 41-47.
- K. Chakraborty, S. Gupta and A. Hoque,
Diophantine triples with the property D(n) for distinct n's,
Mediterr. J. Math. 20 (2023), Article 31, (13pp)
- M. Sadek and T. Yesin,
Divisibility by 2 on quartic models of elliptic curves and rational Diophantine D(q)-quintuples,
Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 116 (2022), Article 139.
- A. Filipin and L. Szalay,
Triangular Diophantine tuples from {1, 2},
Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 27 (2023), 55-70.
- K. N. Adédji, M. Bliznac Trebješanin, A. Filipin and A. Togbé,
On the D(4)-pairs {a,ka} with k ∈ {2,3,6},
Glas. Mat. Ser. III 58 (2023), 35-57.
- M. N. Deshpande,
Wonderland of Families of Diophantine triples, Second Edition, Nagpur, 2022.
- K. Chakraborty, S. Gupta and A. Hoque,
On a conjecture of Franusic and Jadrijevic: Counter-examples,
Results Math. 78 (2023), Article 18.
- A. Filipin and A. Jurasic,
On the existence of D(-3)-quadruples over Z,
Glas. Mat. Ser. III 57 (2022), 203-219.
- M. Kazalicki,
Quadratic twists of genus one curves and Diophantine quintuples,
Res. Number Theory 11 (2025), Article number 72, (19pp)
- S. Bhattacharjee, A. B. Dixit and D. Saikia,
An effective bound on generalized Diophantine m-tuples,
Bull. Aust. Math. Soc. 109 (2024), 242-253.
- M. Le and A. Srinivasan,
A note on Dujella's unicity conjecture,
Glas. Mat. Ser. III 58 (2023), 59-65.
- M. Bliznac Trebješanin and S. Bujačić,
Polynomial D(4)-quadruples over Gaussian integers,
Glas. Mat. Ser. III 59 (2024), 1-31.
- F. Luca and L. Szalay,
Diophantine triples with distinct binary recurrences,
Carpathian J. Math. 39 (2023), 255-264.
- J. M. Mouanda,
On Diophantine m-tuples over the set of commutative matrices,
preprint, 2022.
- J. M. Mouanda,
On matrix Diophantine quadruples which cannot be extended to matrix Diophantine quintuples,
preprint, 2022.
- J. M. Mouanda,
On matrix strong Diophantine 20-tuples,
preprint, 2023.
- I. E. Shparlinski,
On the number of Diophantine m-tuples in finite fields,
Finite Fields Appl. 90 (2023), Paper No. 102241
- J. Park,
Integer points on the elliptic curve with Fibonacci numbers,
Indian J. Pure Appl. Math. 55 (2024), 480-488.
- K. Chakraborty, S. Gupta, A. Hoque,
Diophantine D(n)-quadruples in Z[√4k+2],
Glas. Mat. Ser. III 59 (2024), 259-276.
- J. Kannan, M. Mahalakshmi and P. Nagajothi,
Contriving of parametric sequences of Diophantine triples satisfying non-identical properties,
in: Shodhgodavari: Advanced Knowledge from Multidisciplinary perspectives in Arts, Science, Humanities and Social Sciences,
Multi Spectrum Publications, Kanyakumari, 2022.
- J. Park,
Complete solution of Diophantine pairs induced by some Fibonacci formula,
Algebra Colloq. 30 (2023), 121-132.
- N. Adzaga, G. Drazic, A. Dujella and A. Petho,
Asymptotics of D(q)-pairs and triples via L-functions of Dirichlet characters,
Ramanujan J. 66 (2025), Article 11, (23pp)
- M. Bliznac Trebješanin and P. Radic,
On extensions of D(4)-triples by adjoining smaller elements,
Publ. Math. Debrecen 106 (2025), 147-168.
- M. Cipu, A. Dujella and Y. Fujita,
Extensions of a Diophantine triple by adjoining smaller elements II,
Period. Math. Hungar. 89 (2024), 54-60.
- K. Santicola,
Linear forms in logarithms, Summer project, University of Warwick, September 2022.
- T. Cai,
Perfect Numbers and Fibonacci Sequences,
World Scientific, Singapore, 2022, Section 4.8, pp. 161-165.
- Y. Fujita and I. Soldo,
On the extendibility of certain D(−1)-pairs in imaginary quadratic rings,
Indian J. Pure Appl. Math. 56 (2025), 156-162.
- Y. Fujita and I. Soldo,
The non-existence of D(−1)-quadruples extending certain pairs in imaginary quadratic rings,
Acta Math. Hungar. 170 (2023), 455-482.
- A. Dujella,
High-rank elliptic curves with given torsion group and some applications,
Number-Theoretic Methods in Cryptology (M. Grzeskowiak, J. Pieprzyk, J. Pomykala, ed.),
Banach Center Publications 126, Institute of Mathematics, Polish Academy of Sciences, Warszawa, 2023, pp. 9-26.
- S. Kim, C. H. Yip and S. Yoo,
Multiplicative structure of shifted multiplicative subgroups and its applications to Diophantine tuples,
Canad. J. Math., to appear.
- M. Cipu and Y. Fujita,
On the length of D(±1)-tuples in imaginary quadratic rings,
Bull. Lond. Math. Soc. 56 (2024), 274-287.
- K. Gyarmati,
Elementary Methods to Combinatorial Number Theory, Lecture notes,
Eötvös Loránd University, 2023, Chapter 4.
- S. Gupta,
Diophantine m-tuples in Quadratic Number Fields, PhD thesis,
Harish-Chandra Research Institute, Prayagraj, 2023.
- C. H. Yip,
Multiplicatively reducible subsets of shifted perfect k-th powers and bipartite Diophantine tuples,
Acta Arith. 218 (2025), 251-271.
- E. J. Barbeau, Power Play, The Mathematical Association of America,
1997, pp. 153-159.
- Z. Franusic and A. Jurasic,
On nonexistence of D(n)-quadruples,
Math. Slovaca 74 (2024), 835-844.
- A. Dujella, M. Kazalicki and V. Petricevic,
Rational Diophantine sextuples with strong pair,
Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 119 (2025), Article 36, (10pp)
- S. Kim, C. H. Yip and S. Yoo,
Explicit constructions of Diophantine tuples over finite fields,
Ramanujan J. 65 (2024), 163-172.
- M. Cipu, Y. Fujita and M. Mignotte,
Diophantine triples with three parameters,
Res. Number Theory 10 (2024), Article number 44.
- E. Barbeau,
Gregarious and reclusive triples. Part A: A visit to the land of Fibonacci,
Crux Mathematicorum 50 (2024), 190-192.
- M. Jukic Bokun and I. Soldo,
Extensions of D(−1)-pairs in some imaginary quadratic fields,
New York J. Math. 30 (2024), 745-755.
- N. Irmak,
On k-generalized Fibonacci Diophantine triples,
Math. Commun. 29 (2024), 203-216.
- K. Brown,
Numbers, 2023, Sections 1.7, 1.9, 1.12, 1.13, 3.2, 3.11, 14.5.
- S. Kim, C. H. Yip and S. Yoo,
Paley-like quasi-random graphs arising from polynomials,
preprint, 2024.
- C. H. Yip and S. Yoo,
F-Diophantine sets over finite fields,
Int. J. Number Theory 21 (2025), 1043-1050.
- C. H. Yip,
Improved upper bounds on Diophantine tuples with the property D(n),
Bull. Aust. Math. Soc. 111 (2025), 428-432.
- A. Dujella,
Diophantine m-tuples and Elliptic Curves,
Springer, Cham, 2024.
- E. Barbeau,
Gregarious and reclusive triples. Part B: A plethora of triples and quadruples,
Crux Mathematicorum 50 (2024), 244-247.
- C. H. Yip,
Topics in arithmetic combinatorics,
PhD Thesis, University of British Columbia, 2024.
- E. Barbeau,
Gregarious and reclusive triples. Part C: Finding triples when some elements are known,
Crux Mathematicorum 50 (2024), 290-293.
- R. Rathbun,
2001 Diophantine sextuples of low height,
Zenodo, 2024, https://doi.org/10.5281/zenodo.13362704
- T. Yesin Elsheikh,
Divisibility of Rational Points on Elliptic Curves and Arithmetic Progressions in Polynomial Dynamical Systems,
PhD thesis, Sabanci University, Istanbul, 2023.
- R. Rathbun,
The search for Diophantine sextuples and a possible septuple,
distributed computing project, 2024, http://www.numbertheory.org/ntw/pdfs/search_for_Diophantine_sextuples.pdf
- A. Dujella,
Triples, quadruples and quintuples which are D(n)-sets for several n's,
in: Class Groups of Number Fields and Related Topics. ICCGNERT 2021, ICCGNERT 2022
(K. Chakraborty, A. Hoque and P. P. Pandey, Eds.),
Springer, Singapore, 2024, pp. 77-92.
- G. McShane,
Diophantine triples and the Ptolemy relation,
preprint, 2024.
- J. Badesa,
On the asymptotics of D(n)-pairs and triples,
Ramanujan J. 67 (2025), Article 101, (33pp)
- J. M. Mouanda and K. K. Vincent,
On matrix strong Diophantine 27-tuples and matrix elliptic curves,
Mathematics and Systems Science 2(2) (2024), Article ID: 2624.
- G. Batta, L. Hajdu and A. Pongracz,
On Diophantine graphs, J. London Math. Soc. (2) 111 (2025), no. 5, Paper No. e70163, 21 pp.
- S. Gupta,
Generalized Diophantine m-tuples: a survey,
in: Class Groups of Number Fields and Related Topics. ICCGNERT 2021, ICCGNERT 2022
(K. Chakraborty, A. Hoque and P. P. Pandey, Eds.),
Springer, Singapore, 2024, pp. 219-234.
- K. Gyarmati,
On Diophantine square tuples,
Fibonacci Quart. 63 (2025), 554-569.
- C. H. Yip,
Multiplicatively irreducibility of small perturbations of the set of shifted k-th powers,
Combinatorica 46 (2026), Article 1, (8pp)
- Z. Franusic and A. Jurasic,
Is there a polynomial D(2X+1)-quadruple?,
An. Stiint. Univ. "Ovidius" Constanta Ser. Mat. 33(2) (2025), 67-88.
- G. Batta, M. Szikszai and Sz. Tengely,
Higher power rational Diophantine tuples,
Ramanujan J. 68 (2025), Article 63, (16pp)
- S. Kim, C. H. Yip and S. Yoo,
f-Diophantine sets over finite fields via quasi-random hypergraphs from multivariate polynomials,
preprint, 2025.
- E. Croot and C. H. Yip,
Diophantine tuples and product sets in shifted powers,
preprint, 2025.
- S. Gupta,
Infinitely many counterexamples of a conjecture of Franusic and Jadrijevic,
Arch. Math. (Basel) 125 (2025), 173-184.
- M. Jukic Bokun and I. Soldo,
Triangular D(−1)-tuples,
Bull. Math. Soc. Sci. Math. Roumanie, to appear.
- A. Filipin, A. Jurasic and L. Szalay,
Extensions of the Triangular D(3)-pair {3,6},
Math. Slovaca 75 (2025), 775-790.
- A. Dujella and L. Szalay,
Four squares from three numbers,
preprint, 2025.
- K. Takahashi,
Higher Diophantine Quadruples and Rational Points of Elliptic Curves,
Master Thesis, Tokyo Metropolitan University, 2010 (in Japanese).
- R. Das, M. Somanath and V. A. Bindu,
Formation of Diophantine three tuples for centered polygonal numbers,
Palestine Journal of Mathematics 14(2) (2025), 100-104.
- E. L. F. Roettger and H. C. Williams,
The Enchantment of Numbers, Springer, Cham, 2025, Chapter 20, pp. 273-275.
- Z. Gu,
A generalization of Diophantine tuples,
preprint, 2025.
- K. Chakraborty, S. Gupta and K. Krishnamoorthy,
Diophantine tuples and integral ideals of Q(√d),
preprint, 2025.
- D. Byeon and C. Fuchs,
Cube Diophantine triples and elliptic curves,
Acta Arith. 222 (2026), 37-42.
- A. Hamtat,
Diophantine triples in triangular numbers,
preprint, 2025.
- Y. Briedj and S. E. Rihane,
On the D(1) extension of the D(-1)-Diophantine triples induced by the
D(-1)-Diophantine pair {1,10},
Acta Math. Hungar. 177 (2025), 73-102.
- M. Bliznac Trebjesanin,
On Diophantine triples containing a triangular number,
preprint, 2025.
- D. Dehainsala and J. M. Mouanda,
On matrix strong Diophantine 540-tuples, matrix elliptic curves and matrix hyperelliptic curves,
Advances in Pure Mathematics 15 (2025), 751-762.
- K. M. Tsang and C. H. Yip,
Bipartite Diophantine tuples and their applications,
Res. Number Theory 12 (2026), Article No. 16.
- D. Dehainsala and J. M. Mouanda,
On matrix strong exponential Diophantine m-tuples of order n,
American Journal of Computational Mathematics 15 (2025), 498-505.
- G. Drazic, M. Kazalicki and R. Mrazovic,
Equidistribution of Diophantine pairs among the equivalence classes of quadratic forms,
preprint, 2025.
- V. Ziegler,
On the existence of {p,q}-Diophantine quadruples and quintuples,
Integers 25 (2025), #A92
- Z. Franusic,
Diophantine m-tuples,
Lecture notes, UNIC Mathematics Summer School 2025, Koc University.
- A. Filipin, A. Jurasic and A. Togbe,
A note on the extension of some triangular Diophantine sets,
An. Stiint. Univ. "Ovidius" Constanta Ser. Mat., to appear.
- M. Jukic Bokun and I. Soldo,
The extendibility of the parametric D(−1)-triples,
Publ. Math. Debrecen 108 (2026), 75-85.
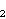 sets, Bull. Calcuta Math. Soc. 86 (1994), 305-306.
sets, Bull. Calcuta Math. Soc. 86 (1994), 305-306.
 with three
non-trivial 2-torsion points, Rocky Mountain J. Math.
30 (2000), 157-164.
with three
non-trivial 2-torsion points, Rocky Mountain J. Math.
30 (2000), 157-164.
 sets, Bull. Calcuta Math. Soc. 86 (1994), 305-306.
sets, Bull. Calcuta Math. Soc. 86 (1994), 305-306.
 with three
non-trivial 2-torsion points, Rocky Mountain J. Math.
30 (2000), 157-164.
with three
non-trivial 2-torsion points, Rocky Mountain J. Math.
30 (2000), 157-164.