x([3] P) = ((6 - 1)/(6 - 4))2 - 4 - 6 = (5
 4)2
- 10 = 5,
4)2
- 10 = 5, y([3] P) = - 1 + (4 - 5)(6 - 1)/(6 - 4) = 0,
[4] P = (6,1), [5] P = (4,6), [6] P =
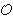 .
.
Primjer: Promotrimo eliptičku krivulju
E : y2 = x3 + x + 3
nad poljem 7.
7.  7). Uočimo da su 0, 1, 2 i 4 svi kvadrati u polju
7). Uočimo da su 0, 1, 2 i 4 svi kvadrati u polju
 7.
Uvrštavamo x = 0, 1, 2, 3, 4, 5, 6 u jednadžbu
krivulje E, te dobivamo redom jednadžbe y2 =
3, 5, 6, 5, 1, 0, 1 u
7.
Uvrštavamo x = 0, 1, 2, 3, 4, 5, 6 u jednadžbu
krivulje E, te dobivamo redom jednadžbe y2 =
3, 5, 6, 5, 1, 0, 1 u  7.
Zaključujemo da samo za x = 4, 5 i 6 pripadne jednadžbe
imaju rješenja. Konačno dobivamo da je
E(
7.
Zaključujemo da samo za x = 4, 5 i 6 pripadne jednadžbe
imaju rješenja. Konačno dobivamo da je
E( 7) =
{
7) =
{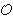 ,
(4,1), (4,6), (5,0), (6,1), (6,6)}.
,
(4,1), (4,6), (5,0), (6,1), (6,6)}.  7).
Uzmimo točku P = (4,1) i izračunajmo njezine višekratnike.
Imamo:
7).
Uzmimo točku P = (4,1) i izračunajmo njezine višekratnike.
Imamo:
x([2] P) = 0 - 8 = 6,
y([2] P) = - 1 + 0 = 6,
x([3] P) = ((6 - 1)/(6 - 4))2 - 4 - 6 =
(5  4)2
- 10 = 5,
4)2
- 10 = 5,
y([3] P) = - 1 + (4 - 5)(6 - 1)/(6 - 4) = 0,
[4] P = (6,1),
[5] P = (4,6),
[6] P = 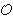 .
.
 7)
je ciklička grupa reda 6, a točka P joj je generator.
7)
je ciklička grupa reda 6, a točka P joj je generator.
Neka je E eliptička krivulja nad konačnim poljem

 .
Postavlja se pitanje što se općenito može reći o grupi
E(
.
Postavlja se pitanje što se općenito može reći o grupi
E(
 ).
Jasno je da za broj elementa na eliptičkoj krivulji vrijedi
#E(
).
Jasno je da za broj elementa na eliptičkoj krivulji vrijedi
#E(
 )
)
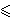 2q + 1.
Naime, imamo jednu točku u beskonačnosti, a pored toga svakom
od q mogućih x-eva odgovaraju najviše dva y-a.
No, samo pola elemenata od
2q + 1.
Naime, imamo jednu točku u beskonačnosti, a pored toga svakom
od q mogućih x-eva odgovaraju najviše dva y-a.
No, samo pola elemenata od 
 imaju kvadratni korijen (to su točno oni elementi koju su oblika
g2n, gdje je g
generator grupe
imaju kvadratni korijen (to su točno oni elementi koju su oblika
g2n, gdje je g
generator grupe

 *), pa možemo očekivati da će
broj #E(
*), pa možemo očekivati da će
broj #E(
 )
biti približno jednak q + 1. Ovo razmatranje je
precizirano u sljedećem važnom teoremu.
)
biti približno jednak q + 1. Ovo razmatranje je
precizirano u sljedećem važnom teoremu.
|
Teorem: (Hasse)
|q + 1 - #E( |
Veličina t definirana sa
#E(
 )
= q + 1 - t naziva se Frobeniusov trag
od E u q. Prema Hasseovom teoremu je
|t|
)
= q + 1 - t naziva se Frobeniusov trag
od E u q. Prema Hasseovom teoremu je
|t| 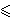 2
2 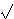 q.
q.
Za eliptičke krivulje nad

 tvrdnja Hasseovog teorema je najbolja moguća, u smislu da
za svaki prirodan broj n iz intervala
(p + 1 - 2
tvrdnja Hasseovog teorema je najbolja moguća, u smislu da
za svaki prirodan broj n iz intervala
(p + 1 - 2
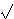 p,
p + 1 + 2
p,
p + 1 + 2
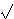 p)
postoji eliptička krivulja reda n. Štoviše,
unutar manjeg intervala
(p + 1 -
p)
postoji eliptička krivulja reda n. Štoviše,
unutar manjeg intervala
(p + 1 -
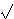 p,
p + 1 +
p,
p + 1 +
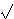 p)
redovi su gotovo uniformno distribuirani. Ova činjenica je
jako važna za neke od primjena eliptičkih krivulja, kao što
faktorizacija velikih prirodnih brojeva, te dokazivanje
prostosti.
p)
redovi su gotovo uniformno distribuirani. Ova činjenica je
jako važna za neke od primjena eliptičkih krivulja, kao što
faktorizacija velikih prirodnih brojeva, te dokazivanje
prostosti.
Napomenimo da računanje reda grupe
E(
 )
za velike brojeve q nije sasvim jednostavan problem.
Prvi polinomijalni algoritam za računanje
#E(
)
za velike brojeve q nije sasvim jednostavan problem.
Prvi polinomijalni algoritam za računanje
#E(
 )
dao je Schoof 1995. godine.
Broj operacija u tom algoritmu je bio O(log8q).
Kasnije su Atkin i
Elkies poboljšali Schoofov algoritam,
tako da se danas broj
#E(
)
dao je Schoof 1995. godine.
Broj operacija u tom algoritmu je bio O(log8q).
Kasnije su Atkin i
Elkies poboljšali Schoofov algoritam,
tako da se danas broj
#E(
 )
može efikasno izračunati za brojeve q s do 500 znamenaka.
)
može efikasno izračunati za brojeve q s do 500 znamenaka.
Pretpostavimo sada da imamo eliptičku krivulju E
zadanu nad 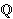 .
Bez smanjenja općinosti možemo pretpostaviti da su joj
koeficijenti cjelobrojni. Stoga za svaki prosti broj p
možemo promatrati ostatke tih koeficijenata pri djeljenju
s p. Na taj način ćemo dobiti krivulju
nad
.
Bez smanjenja općinosti možemo pretpostaviti da su joj
koeficijenti cjelobrojni. Stoga za svaki prosti broj p
možemo promatrati ostatke tih koeficijenata pri djeljenju
s p. Na taj način ćemo dobiti krivulju
nad 
 koja će biti eliptička ukoliko je nesingularna, a to će biti
ukoliko p ne dijeli diskriminantu D od E.
Podsjetimo se da je jedno od važnih pitanja vezanih uz
eliptičke krivulje nad
koja će biti eliptička ukoliko je nesingularna, a to će biti
ukoliko p ne dijeli diskriminantu D od E.
Podsjetimo se da je jedno od važnih pitanja vezanih uz
eliptičke krivulje nad 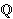 određivanje njihovog ranga. Jedna od najpoznatijih
i najvažnijih slutnji u matematici jest
Birch -
Swinnerton-Dyerova slutnja
koja povezuje rang eliptičke krivulje nad
određivanje njihovog ranga. Jedna od najpoznatijih
i najvažnijih slutnji u matematici jest
Birch -
Swinnerton-Dyerova slutnja
koja povezuje rang eliptičke krivulje nad
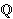 s brojem točaka na toj istoj krivulji kad se ona
promatra nad konačnim poljem
s brojem točaka na toj istoj krivulji kad se ona
promatra nad konačnim poljem 
 .
Ugrubo rečeno, za eliptičku krivulju velikog ranga bi brojevi
#E(
.
Ugrubo rečeno, za eliptičku krivulju velikog ranga bi brojevi
#E(
 )
trebali biti relativno veliki za mnogo prostih brojeva p.
Preciznije,
)
trebali biti relativno veliki za mnogo prostih brojeva p.
Preciznije, 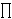 (#E(
(#E(
 ) / p),
gdje se produkt uzima po svim prostim brojevima p
koji ne dijele diskriminantu, a manji su od realnog broja X,
je proporcionalan sa (log X)r,
gdje je r upravo rang krivulje E.
Još preciznija formulacija Birch - Swinnerton-Dyerove slutnje
je preko tzv. L-funkcija, te kaže da je rang jednak redu
nultočke jedne analitičke funkcije koja se definira pomoću
brojeva #E(
) / p),
gdje se produkt uzima po svim prostim brojevima p
koji ne dijele diskriminantu, a manji su od realnog broja X,
je proporcionalan sa (log X)r,
gdje je r upravo rang krivulje E.
Još preciznija formulacija Birch - Swinnerton-Dyerove slutnje
je preko tzv. L-funkcija, te kaže da je rang jednak redu
nultočke jedne analitičke funkcije koja se definira pomoću
brojeva #E(
 ).
).
Za razliku od slučaja eliptičkih krivulja nad
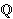 ,
gdje je otvoreno pitanje koji su sve rangovi mogući,
u slučaju polja
,
gdje je otvoreno pitanje koji su sve rangovi mogući,
u slučaju polja 
 poznato je
da je pripadna grupa ili ciklička ili produkt dvije cikličke grupe.
Preciznije, vrijedi
poznato je
da je pripadna grupa ili ciklička ili produkt dvije cikličke grupe.
Preciznije, vrijedi
E(
 )
)
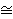
 d
×
d
×
 e,
e,
U dosadašnjim razmatranjima, mi smo se uglavnom ograničili na
eliptičke krivulje nad poljima karakteristike različite od 2 i 3.
Međutim, kako su za primjene u kriptografiji od velike važnosti
eliptičke krivulje nad konačnim poljima karakteristike jednake 2,
sada ćemo reći nešto o njima.
Svaka eliptička krivulja nad poljem

 ,
gdje je q = 2m, može se
transformirati u jedan od sljedeća dva oblika
y2 + cy = x3 +
ax + b ili
y2 + xy = x3 +
ax2 + b.
Međutim, krivulje prvog oblika su tzv. supersingularne krivulje,
koje nisu, iz razloga koje ćemo kasnije objasniti,
od interesa kod primjene u kriptografiji. Stoga se možemo
usredotočiti na krivulje drugog oblika. Pritom je
b proizvoljan ne-nul element iz
,
gdje je q = 2m, može se
transformirati u jedan od sljedeća dva oblika
y2 + cy = x3 +
ax + b ili
y2 + xy = x3 +
ax2 + b.
Međutim, krivulje prvog oblika su tzv. supersingularne krivulje,
koje nisu, iz razloga koje ćemo kasnije objasniti,
od interesa kod primjene u kriptografiji. Stoga se možemo
usredotočiti na krivulje drugog oblika. Pritom je
b proizvoljan ne-nul element iz

 ,
dok za a imamo samo dvije bitno različite (koje daju
neizomorfne krivulje) mogućnosti: a = 0 ili
a =
,
dok za a imamo samo dvije bitno različite (koje daju
neizomorfne krivulje) mogućnosti: a = 0 ili
a = 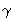 ,
gdje je
,
gdje je 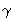 neki fiksirani element iz
neki fiksirani element iz

 sa svojstvom da je Tr(
sa svojstvom da je Tr(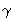 ) =
) =
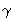 +
+
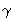 2 +
2 +
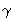 4 +
... +
4 +
... +
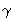 2
2

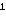 = 1.
Ako je m neparan, onda možemo uzeti da je
= 1.
Ako je m neparan, onda možemo uzeti da je
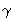 = 1.
= 1.
Navedimo još formule za zbrajanje točaka na eliptičkoj krivulji zadanoj jednadžbom y2 + xy = x3 + ax2 + b nad poljem karakteristike 2. Ako je P = (x1, y1) i Q = (x2, y2), onda je
-P = (x1, x1 +
y1),
x(P + Q) = ((y2 +
y1) /
(x2 + x1))2
+ (y2 +
y1) /
(x2 + x1)
+ a + x1 + x2,
y(P + Q) = y1 +
x(P + Q) +
(x1 + x(P + Q))
(y2 +
y1) / (x2 + x1),
x([2]P) =
((x12 + y1) /
(x1))2 +
(x12 + y1) /
(x1) + a,
y([2]P) = y1 +
x([2]P) +
(x1 + x([2]P))
(x12 + y1) /
(x1).

 )
za q = 3, 5, 7, 9, 11.
)
za q = 3, 5, 7, 9, 11.
 5
je jedan od brojeva n = 2, 3, ... , 10.
Za svaki od mogućih n-ova, pronađite jednu eliptičku
krivulju nad
5
je jedan od brojeva n = 2, 3, ... , 10.
Za svaki od mogućih n-ova, pronađite jednu eliptičku
krivulju nad
 5
čiji je red upravo jednak n.
5
čiji je red upravo jednak n.
| Web stranica seminara | Andrej Dujella - osobna stranica |