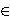 K) kubni polinom bez višestrukih korijena.
Eliptička krivulja E nad
K je skup svih točaka (x, y)
K) kubni polinom bez višestrukih korijena.
Eliptička krivulja E nad
K je skup svih točaka (x, y)
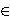 K × K koje zadovoljavaju jednadžbu
K × K koje zadovoljavaju jednadžbu
y2 = x3 + ax + b,
zajedno s još jednim elementom kojeg označavamo s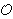 i zovemo
"točka u beskonačnosti".
i zovemo
"točka u beskonačnosti".
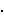 1 = 0, gdje su 0 i 1
neutralni elementi za zbrajanje, odnosno množenje u K.
Ako je n
1 = 0, gdje su 0 i 1
neutralni elementi za zbrajanje, odnosno množenje u K.
Ako je n 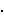 1
1
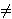 0
za svaki prirodan broj n, onda se kaže da je
K polje karakteristike 0. Pojam eliptičke krivulje se
može definirati nad proizvoljnim poljem K, međutim najvažniji
slučajevi su kad je K polje racionalnih brojeva
0
za svaki prirodan broj n, onda se kaže da je
K polje karakteristike 0. Pojam eliptičke krivulje se
može definirati nad proizvoljnim poljem K, međutim najvažniji
slučajevi su kad je K polje racionalnih brojeva
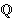 ,
polje realnih brojeva
,
polje realnih brojeva
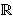 ,
polje kompleksnih brojeva
,
polje kompleksnih brojeva
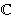 ,
te konačno polje
,
te konačno polje 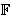
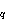 od q elemenata. Polja
od q elemenata. Polja
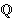 ,
,
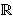 i
i
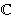 su karakteristike 0,
dok je karakteristika od
su karakteristike 0,
dok je karakteristika od
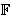
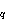 jednaka p, gdje je p prost broj i q =
pm za neki prirodan broj m.
jednaka p, gdje je p prost broj i q =
pm za neki prirodan broj m.
Definicija:
Neka je K polje
karakteristike različite od 2 i 3, te neka je f(x) = x3 +
ax + b (gdje su a, b
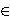 K) kubni polinom bez višestrukih korijena.
Eliptička krivulja E nad
K je skup svih točaka (x, y) K) kubni polinom bez višestrukih korijena.
Eliptička krivulja E nad
K je skup svih točaka (x, y)
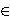 K × K koje zadovoljavaju jednadžbu
K × K koje zadovoljavaju jednadžbu
y2 = x3 + ax + b, zajedno s još jednim elementom kojeg označavamo s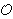 i zovemo
"točka u beskonačnosti". i zovemo
"točka u beskonačnosti".
|
Uvjet da polinom f(x) nema višestrukih
korijena ekvivalentan je uvjetu da je
4a3 + 27b2 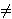 0.
Broj D = - 4a3 - 27b2
se zove diskriminanta polinoma f(x).
Nije teško provjeriti da ako su x1,
x2 i x3 (kompleksne)
nultočke od f, onda je D =
(x1 - x2)2
(x1 - x3)2
(x2 - x3)2.
0.
Broj D = - 4a3 - 27b2
se zove diskriminanta polinoma f(x).
Nije teško provjeriti da ako su x1,
x2 i x3 (kompleksne)
nultočke od f, onda je D =
(x1 - x2)2
(x1 - x3)2
(x2 - x3)2.
Slično se može definirati eliptička krivulja i nad poljima karakteristike 2 ili 3. Ako je char K = 3, onda je pripadna jednadžba y2 = x3 + ax2 + bx + c, a ako je char K = 2, onda imamo dva tipa jednadžbi: y2 + cy = x3 + ax + b ili y2 + xy = x3 + ax2 + b.
Opći oblik jednadžbe (koji je dobar nad svakim poljem) je:
y2 + a1xy + a3y = x3 + a2x2 + a4x + a6.
Ovu jednadžbu zovemo Weierstrassova forma od E i ona se supstitucijom varijabli (nadopunom na potpun kvadrat i potpun kub) može transformirati do jedne od gore navedenih jednadžbi, koju onda zovemo kratka Weierstrassova forma od E. U slučaju ove opće jednadžbe, umjesto uvjeta o različitim korijenima, imamo uvjet da su sve točke na krivulji nesingularne (to znači da je u svakoj točki barem jedna od parcijalnih derivacija 0,
tj. da u svakoj točki postoji tangenta).
0,
tj. da u svakoj točki postoji tangenta).
Jedno od najvažnijih svojstava eliptičkih krivulja jest da se na
njima može, na prirodan način, uvesti operacija uz koju one
postaju abelove grupe. Da bi to objasnili, uzmimo da je K =
 polje realnih brojeva.
Tada eliptičku krivulju (bez točke u beskonačnosti)
možemo prikazati kao podskup ravnine.
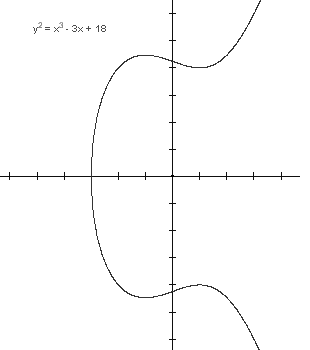
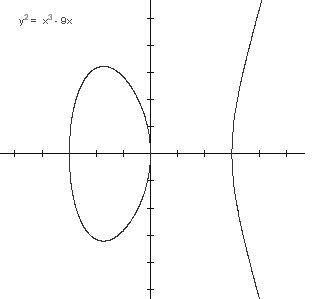
Polinom f(x) može imati 1 ili 3 realna korijena.
U ovisnosti o tome, graf pripadne eliptičke
krivulje ima jednu ili dvije komponente, kao što je
prikazano na sljedećim slikama.
polje realnih brojeva.
Tada eliptičku krivulju (bez točke u beskonačnosti)
možemo prikazati kao podskup ravnine.
Polinom f(x) može imati 1 ili 3 realna korijena.
U ovisnosti o tome, graf pripadne eliptičke
krivulje ima jednu ili dvije komponente, kao što je
prikazano na sljedećim slikama.
|
|
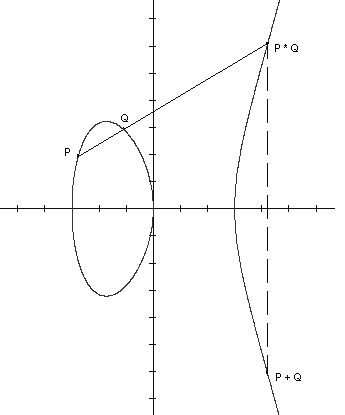
Definirat ćemo operaciju zbrajanja na E.
Neka su P, Q
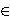 E.
Povucimo pravac kroz točke P i Q. On siječe
krivulju E u tri točke. Treću točku
označimo s P * Q. Sada definiramo da je
P + Q osnosimetrična točka točki P * Q
s obzirom na os x (vidi sliku).
E.
Povucimo pravac kroz točke P i Q. On siječe
krivulju E u tri točke. Treću točku
označimo s P * Q. Sada definiramo da je
P + Q osnosimetrična točka točki P * Q
s obzirom na os x (vidi sliku).
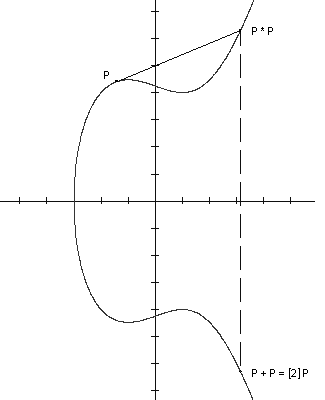
Ako je P = Q,
onda umjesto sekante povlačimo tangentu kroz
točku P. Po definiciji stavljamo da je
P + 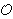 =
=
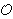 + P
= P za svaki P
+ P
= P za svaki P
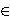 E.
E.
|
|
Pokazuje se da skup E uz ovako definiranu operaciju
zbrajanja postaje abelova grupa. Očito je
 neutralni
element, dok je -P osnosimetrična točka točki P u
odnosu na os x. Komutativnost je također očita.
Najteže je provjeriti asocijativnost. To se
može napraviti korištenjem eksplicitnih formula za
zbrajanje, koje ćemo sada navesti.
neutralni
element, dok je -P osnosimetrična točka točki P u
odnosu na os x. Komutativnost je također očita.
Najteže je provjeriti asocijativnost. To se
može napraviti korištenjem eksplicitnih formula za
zbrajanje, koje ćemo sada navesti.
Ako je P = (x1, y1) i Q = (x2, y2), onda je
x(P + Q) = ((y2 -
y1) /
(x2 - x1))2
- x1 - x2,
y(P + Q) = -y1 +
(x1 - x(P + Q))
(y2 -
y1) / (x2 - x1),
x([2]P) =
((3x12 + a) /
(2y1))2
- 2x1,
y([2]P) = -y1 +
(x1 - x([2]P))
(3x12 + a) /
(2y1).
 . Ona se pojavljuje
prirodno ukoliko eliptičku krivulju prikažemo u projektivnoj
ravnini. Projektivnu ravninu dobijemo tako što na
skupu
. Ona se pojavljuje
prirodno ukoliko eliptičku krivulju prikažemo u projektivnoj
ravnini. Projektivnu ravninu dobijemo tako što na
skupu 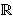
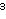 \ {(0,0,0)} uvedemo relaciju ekvivalencije
(kX, kY, kZ) ~ (X, Y, Z),
za k
\ {(0,0,0)} uvedemo relaciju ekvivalencije
(kX, kY, kZ) ~ (X, Y, Z),
za k 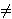 0.
Ako u jednadžbi eliptičke krivulje (koju nazivamo još i afina jednadžba) uvedemo supstituciju
x = X / Z,
y = Y / Z, dobivamo projektivnu jednadžbu
eliptičke krivulje
0.
Ako u jednadžbi eliptičke krivulje (koju nazivamo još i afina jednadžba) uvedemo supstituciju
x = X / Z,
y = Y / Z, dobivamo projektivnu jednadžbu
eliptičke krivulje
Y2Z = X3 + aXZ2 + bZ3.
Ako je Z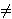 0,
onda klasa od (X, Y, Z) ima reprezentant
oblika (x, y, 1), pa ju možemo identificirati
sa (x, y). Međutim, postoji i jedna klasa
ekvivalencije koja sadrži točke za koje je Z = 0.
Ona ima reprezentant (0, 1, 0) i nju identificiramo s
točkom
0,
onda klasa od (X, Y, Z) ima reprezentant
oblika (x, y, 1), pa ju možemo identificirati
sa (x, y). Međutim, postoji i jedna klasa
ekvivalencije koja sadrži točke za koje je Z = 0.
Ona ima reprezentant (0, 1, 0) i nju identificiramo s
točkom 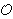 .
.
Uočimo da je u točkama u kojima eliptička krivulja siječe
os x, tangenta okomita na os x. Treća točka
presjeka tog pravca s E je
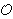 . To znači da
za te točke vrijedi [2] P =
. To znači da
za te točke vrijedi [2] P =
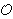 , pa kažemo da su
to točke reda 2 ili 2-torzijske točke.
, pa kažemo da su
to točke reda 2 ili 2-torzijske točke.
Jasno je da gore navedene algebarske formule za zbrajanje točaka,
koje smo dobili za slučaj eliptičke krivulje nad
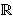 , imaju smisla
nad svakim poljem (uz malu modifikaciju za slučaj polja s
karakteristikom 2 i 3). Pokazuje se da uz operaciju definiranu
ovim formulama eliptička krivulja nad proizvoljnim poljem K
postaje abelova grupa.
, imaju smisla
nad svakim poljem (uz malu modifikaciju za slučaj polja s
karakteristikom 2 i 3). Pokazuje se da uz operaciju definiranu
ovim formulama eliptička krivulja nad proizvoljnim poljem K
postaje abelova grupa.
(x1 - x2)2 (x1 - x3)2 (x2 - x3)2 = - 4a3 - 27b2.
y2 = x3 + ax2 + bx + c.
y2 = x3 - 43x + 166,
tj. najmanji prirodan broj n takav da je [n] P = P + ... + P = .
.
| Web stranica seminara | Andrej Dujella - osobna stranica |