Potpuni zastoji (deadlocks)

 

Već smo primjetili da potpuni zastoj može nastati kad postoji pokušaj sinkroniziranja procesa u radu sa zajedničkom memorijom, semaforima i sl. Ovaj koncept se može generalizirati kad procesi dijele bilo koju vrstu resursa. Formalno potpuni zastoj možemo definirati na sljedeći način:

 

Skup procesa se nalazi u stanju potpunog zastoja ako svaki proces u skupu čeka na neki događaj koji može proizvesti jedino neki proces iz tog skupa.

 

Uvjeti za nastajanje potpunog zastoja:

 

Potpuni zastoj može nastati ako su prisutna sva četiri dolje navedena uvjeta.

 

  1. Stanje međusobnog isključivanja. Svaki resurs je ili pridružen nekom procesu ili je slobodan.
  2. Stanje prisvajanja i čekanja (hold and wait condition). Procesi koji su dobili (i drže) neke resurse zahtijevaju nove resurse.
  3. Nema oduzivih resursa[1]. Resursi prethodno rezervirani ne mogu biti oduzeti procesu. Proces koji ih drži mora ih eksplicitno otpustiti.
  4. Kružno čekanje. Mora postojati ciklus od dva ili više procesa, od kojih svaki čeka resurs koji je dodijeljen sljedećem članu ciklusa.

 

Ako jedan od ovih uvjeta nedostaje potpuni zastoj nije moguć.

 

Modeliranje potpunog zastoja

 

Alokaciju resursa možemo modelirati koristeći grafove. Krugovi će reprezentirati procese, kvadrati će reprezentirati resurse, dok će luk između procesa i resursa označavati da proces čeka na taj resurs, odnosno da je resurs dodijeljen procesu (ako je smjer luka od resursa prema procesu). Ako prilikom modeliranja grafa dobijemo ciklus to će ukazati da je potpuni zastoj moguć.

Npr. na slici su prikazana sljedeća stanja:

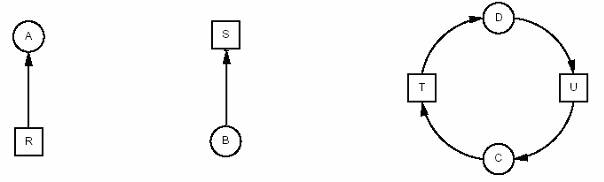
Resurs R je dodijeljen procesu A. Proces B čeka na resurs S. Na trećoj slici vidimo potpuni zastoj. Proces C čeka resurs T koji je dodijeljen procesu D. Proces D neće otpustiti resurs T jer čeka resurs U kojeg drži proces C. U ovom primjeru ciklus je C-T-D-U-C.

 

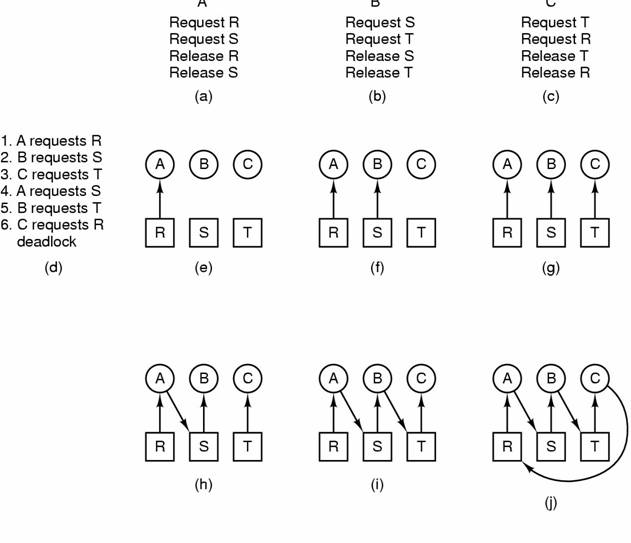
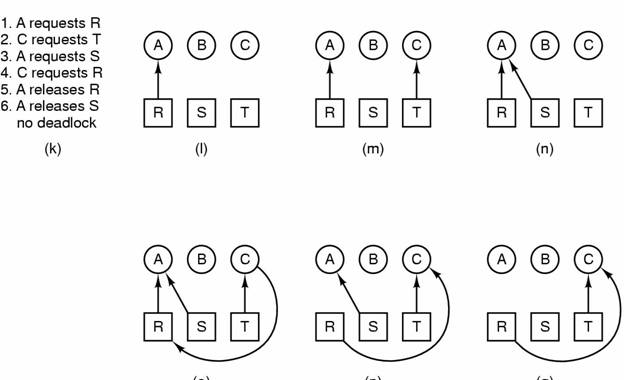
Crtajući graf sustava možemo pronaći ciklus koji odgovara izvođenju procsa kao na prvom dijelu slike.  ( ...graf...)

 

Zadatak: Dva procesa A i B trebaju 3 zapisa (1,2,3) u nekoj bazi podataka. Ako A traži ekskluzivni pristup do njih u redoslijedu 1,2,3 i B traži u istom potpuni zastoj nije moguć. Međutim ako B traži u redoslijedu 3,2,1 može doći do potpunog zastoja. Koje sve kombinacije i koliko ih ima su dozvoljene kako bi bili sigurni da neće doći do potpunog zastoja.

 

 

Što sa potpunim zastojima? Općenito četiri strategije se koriste za rukovanje sa potpunim zastojima:

  1. Ignoriranje problema
  2. Otkrivanje i oporavak. Neka se potpuni zastoj dogodi, bude otkriven i onda se poduzima određena akcija
  3. Dinamičko izbjegavanje pažjivom alokacijom resursa
  4. Sprječavanje, pokušajem negiranja jednog od 4 uvjeta za nastajanje potpunog zahtjeva.

 

Nojev algoritam

 

Ako je vjerojatnost pojave potpunog zastoja mala ili je šteta u slučaju potpunog zastoja zanemariva onda sprječavanje potpunog zastoja možda nije vrijedno komplikacija i restrikcija u operacijskih sustavima. (Windowsi i Unix koriste ovaj princip)

 

Detektiranje potpunog zastoja i oporavak

 

Mana ovog pristupa je što treba održavati grafove alokacije resursa koji mogu biti veliki i poprilično složeni , pa i sam algoritam može biti 'skup'.

 

Otkrivanje potpunog zastoja sa jednim resursom pojedinog tipa resursa

Algoritam koji bi dao rješenje da li se može dogoditi potpuni zastoj u ovakvom slučaju sveo bi se na traženje ciklusa u grafu i mogao bi se zapisati ovako:

  1. Za svaki čvor N u grafu obavi sljedećih 5 koraka sa N kao startnim čvorom
  2. Inicijaliziraj L na praznu listu i označi sve lukove kao neoznačene
  3. Dodaj trenutni čvor na kraj liste L i provjeri da li se čvor nalazi dvaput u listi. Ako da graf sadrži ciklus pa je algoritam završen.
  4. Od zadanog čvora pogledaj da li ima još neoznačenih lukova. Ako da pređi na korak 5, inače idi na korak 6.
  5. Uzmi bilo koji neoznačeni čvor i označi ga. Prijeđi u taj čvor i idi na korak 3.
  6. Algoritam je naišao na čvor na kraju. Makni ga iz liste i idi na čvor prethodno zapisan u listi te nakon toga prijeđi na korak 3. Ako je taj čvor startni čvor algoritam ne sadrži ciklus te ponovi algoritam sa nekim drugim startnim čvorom..

 

Kako algoritam radi protrimo na sljedećem grafu:

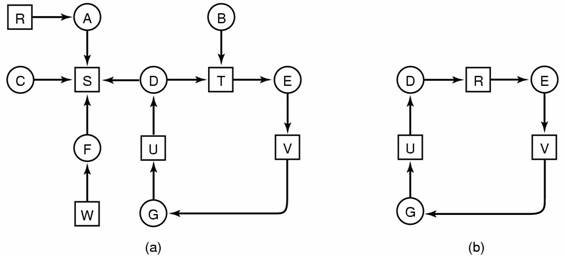
Neka algoritam krene za startne čvorove ima redom R,A,B,C,S ...Krenemo iz čvora R i inicijaliziramo praznu listu. Dodamo R i odemo na sljedeći mogući čvor A, pa je lista L=[R,A]. Iz A idemo u S => L=[R,A,S]. Iz S ne izlazi ni jedan luk, pa ga brišemo iz liste i vraćamo se u A. Kako ni iz A nema neoznačenih lukova vraćamo se u R, a to je startni čvor i algoritam pokrećemo sa novim startnim čvorom A. L ispraznimo i ponovimo postupak koji brzo završi. Kada krenom iz B nakon nekoliko koraka dobit ćemo listu L=[B,T,E,V,G,U,D]. Nakon toga slučajnim odabirom izaberemo između S (taj korak brzo završi) i T, što daje listu L=[B,T,E,V,G,U,D,T] što ukazuje na ciklus.

 

Otkrivanje potpunog zastoja sa više resursa istog tipa

Kada postoji više kopija istog resursa onda je potreban drugačiji pristup. Neka su procesi označeni sa P1 do Pn. Neka je broj tipova resursa m, i to neka je Ei broj resursa tipa resursa i (1<=i<=m). E je vektor postojećih resursa. U bilo kojem trenutku neki resursi su dodijeljeni a neki su slobodni. Neka A predstavlja vektor slobodnih resursa.Neka matrica C predstavlja trenutno zauzete (alociranih) resursa na način da Cij predstavlja broj resursa tipa j koji su dodijeljeni procesu i te neka R na sličan način predstavlja matricu potraživanja.

Pritom mora vrijediti + Aj = Ej

 

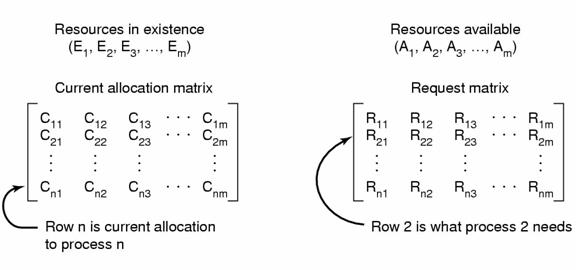
Algoritam za otkrivanje potpunog zastoja bazira se na usporedbi vektora. Definirajmo relaciju <= na dva vektora A i B ovako: A<=B ako i samo ako Ai<=Bi za svako 1 <= i <= m, pa je algoritam sljedeći:

  1. Potraži bilo koji neoznačeni procesa Pi, za koji je i-ti redak matrice R manji ili jednak A
  2. Ako takav proces postoji dodaj i-ti redak matrice C vektoru A, označi proces i idi na korak 1.
  3. Ako takav proces ne postoji završi algoritam.

 

Kada algoritam završi svi neoznačeni procesi, ako postoje, su u stanju potpunog zastoja.

 

Primjer:

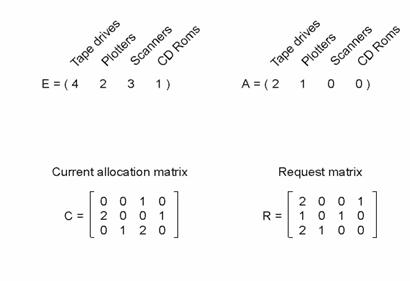
Zahtjev trećeg procesa može biti zadovoljen, pa kad završi njegovi će resursi biti oslobođeni pa će A biti (2 2 2 0) pa će moći i proces 2 biti izvršen nakon čega je A=(4 2 2 1) pa i prvi proces može biti izvšeni , tj . nema potpunog zastoja u ovom slučaju.

 

 

 Oporavak od potpunog zastoja

Za oporavak od potpunog zastoja možemo napraviti sljedeće:

-         oduzimanje resursa i naknadno vraćanje – ponekad nije moguće izvršiti

-         rollback – periodično se stvara checkpoint (sadrži stanje memorije i stanja resursa). Prilikom detektiranja zastoja lako se vidi koji resurs je potreban. Proces koji drži taj resurs se vraća na jedan od prethodnih chekpointa u kojem još nije prisvojio traženi resurs

-         oporavak ubijanjem procesa – najednostavnije je 'ubiti' proces unutar ciklusa. Uz malo sreće ostali procesi će moći nastaviti rad, inače postupak ponoviti. Kada je to moguće poželjno je 'zaustaviti' proces koji se može ponovo izvesti bez posljedica.

 

Izbjegavanje potpunog zastoja

 

U prethodnim razmatranjima pretpostavljalo se da procesi sve potrebne resurse traže odjednom. Međutim u stvarnosti resursi se traže jedan po jedan. Pitanje koje se postavlja je: Da li postoji algoritam koji bi uvijek izbjegavao potpuni zastoj čineći prave odluke u svakom trenutku. Odgovor je da, ali ako su unaprijed poznate određene informacije. Izbjegavanje se razlikuje od sprječavanja jer donosi odluke bazirane na zahtjevu za svaki pojedini resurs umjesto postavljanja strogih uvjeta na sve resurse. Glavni algoritam za izbjegavanje potpunog zastoja je baziran na konceptu sigurnih stanja. Da bi lakše objasnili pojam sigurnog stanja promotrimo sljedeću sliku: (objašnjenje slike ... )

 

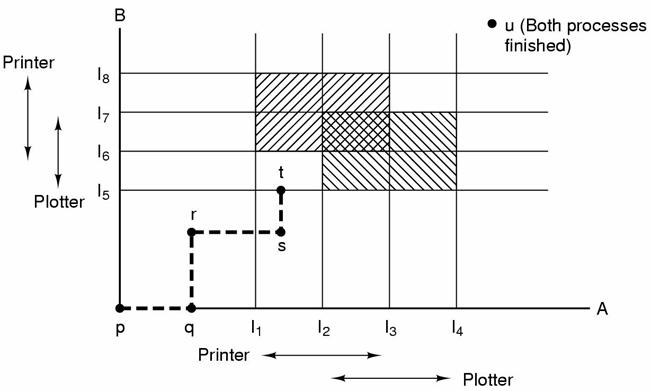
Neka u trenutku I1 proces A zahtjeva printer i u trenutku I2 zahtjeva ploter, koji se otpuštaju u trenutcima I3 i I4. Proces B treba printer od I5 do I7 i printer od I6 do I8. Svaka točka na dijagramu predstavlja stanje obaju procesa. Unutar jednoprocesorskog računala putovi u grafu moraju biti ili horizontalni ili vertikalni. Na putu od točke r do s, proces A je zatražio i dobio pristup printeru. Kada proces B dođe do točke t, on zahtjeva ploter. Osjenčane regije prikazuje stanja kad oba procesa imaju ploter , odnosno kad oba procesa imaju printer. Međusobno isključivanje čini takva stanje nemogućim, tj. ne dozvoljava ulaz u ta područja.

Ako sustav ikad stane na rub područja omeđenog sa I1 - I2 i sa I5 - I6, postoji mogućnost potpunog zastoja ako daljnim izvršavanjem dođe na presjek I2 i I6 . (u tom trenutku A bio ima printer i tražio ploter, B obrnuto). Jedina sigurna stvar u trenutku t je da se proces A izvršava sve dok ne dođe do I4 . Bitna stvar je primjetiti da u točki t B zahtjeva resurs i sustav treba odlučiti da li mu ga dozvoliti ili ne. Ako bi dozvolio, onda bi se sustav našao u nesigurnom stanju.

Stanje nazivamo sigurnim ako u njemu nije nastao potpuni zastoj i ako postoji neki algoritam raspoređivanja procesa u kojem svaki od procesa može završiti svoje izvođenje čak i ako svi od procesa odmah zatraže njihov maksimalan broj resursa.

 

Promotrimo sljedeći primjer:

Neka proces A ima 3 instance resursa, a eventulano će trebati do 9 resursa. B neka trenutno ima 2 resursa i možda treba do 4 resursa, dok C ima 2 resursa, a maksimalno treba 7 resusra. Neka ukupno postoji 10 resursa, iz čega sljedi da su trenutno 3 slobodna.

 

 

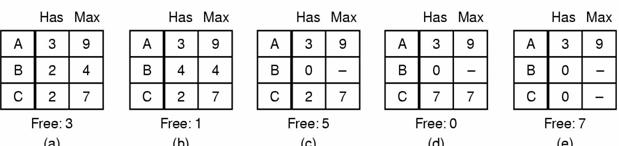
Na gornjoj slici sva stanja su sigurna. No da je npr. u stanju a proces A zatražio i dobio još jedan resurs to bi nas mogo dovesti do sljedećeg stanja:

 

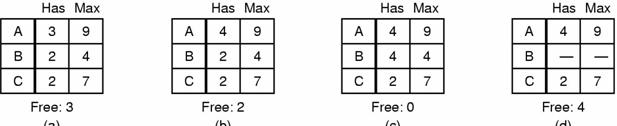Iz slike možemo vidjeti da smo u tom slučaju već u prvom koraku prešli u nesigurno stanje. Što znači da zahtjev procesa A nije smio biti odobren.

Treba napomenuti da nesigurno stanje ne mora nužno biti i stanje koje vodi u potpuni zastoj (npr. A je mogao nakon nekog vreemena otpustiti neke resusrse).

 

Algoritam raspoređivanja koji izbjegava potpuni zastoj osmislio je Dijkstra (1965.) i poznat je kao bankarev algoritam. Problem je modeliran na način da se razmatra bankar u malom gradu koji radi sa grupom klijenata kojima odobrava kredite. Bankar zna da svi klijenti neće odjednom tražiti kredit, pa će rezervirati samo dio novca umjesto čitave moguće svote koja se može potraživati. Kredit će odobriti ako će situacija u koju se prelazi davanjem pojedinog kredita biti sigurna situacija, inače kredit se odgađa. Kako bi vidio da li je stanje sigurno bankar provjerava da li ima dovoljno resursa (novaca) da zadovolji nekog klijenta. Ako da, pretpostavlja se da će ti zajmovi biti vraćeni, pa se provjerava klijent najbliži limitu itd. Ako svi zajmovi mogu biti obavljeni pretpostavlja se da je stanje sigurno i da zahtjev moež biti odobren.

 

Bankarev algoritam može biti generaliziran na više tipova resursa. Donja slika pokazuje na koji način to radi:

 

 

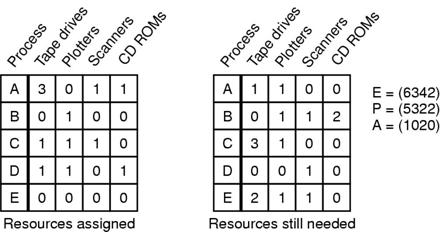
Na slici vidimo dvije matrice. Lijeva matrica pokazuje koliko pojedinih resursa je trenutno dodijeljeno svakom od 5 procesa. Matica sa desne strane govori koliko resursa svaki od procesa treba. Ove dvije matrice su zapravo matrice C i R iz prethodnih razmatranja. Kao i kod prethodnog slučaja sa jednim tipom resursa, procesi moraju prije početka izvršavanja iskazati koliko resursa trrebaju kako bi sustav znao formirati desnu matricu. Vektori E,P i A predstavljaju broj postojećih resursa, broj zauzetih resursa (od strane procesa) te broj slobodnih resursa). Algoritam koji provjerava da li je neko stanje sigurno je:

 

  1. Pronađi redak R u kojem su sve vrijednosti manje ili jednake vrijednostima u vektoru A. Ako takav redak ne postoji sustav će biti  u stanju potpunog zastoja jer nijedan proces ne može nastaviti svoje izvršavanje.
  2. Pretpostavimo da proces iz odabranog retka zahtjeva sve resurse koje treba i završi. Označi proces kao završen i pridodaj njegove sve njegove resurse vektoru A.
  3. Ponovi korake 1 i 2 dok svi procesi ne postanu označeni kao završeni (u tom slučaju stanje je sigurno) ili dok se ne pojavi potpuni zastoj (u tom slučaju stanje nije sigurno)

 

Promotrimo ponovo gornju sliku. Ako B zahtjeva printer zahtjevu se može udovoljiti jer novo stanje je i dalje sigurno (D može završiti, zatim A ili E itd.. ) Ako bi nakon B, E tražio zadnji printer odobravanje tog zahtjeva vodilo bi na stanje slobodnih resursa (1 0 0 0) što dovodi do potpunog zastoja.

 

Nažalost bankarski algoritam je jako dobar teoretski primjer, nažalost teško ostvariv u praksi jer većina procesa dinamički treba resurse, tj. ne zna te podatke prije početka izvršavanja.

 

Sprječavanje potpunog zastoja

 

Spječavanje potpunog zastoja se zasniva na sljedećim idejama: napadanje međusobnog isključivanja, napadanje hold and wait uvjeta (npr. zahtjevaj sve resurse odjednom), napadanje neoduzivih resursa ili napadanje ciklusa čekanja (npr. numeriranjem resursa).

 

 

U nekim bazama podataka koristi se zaključavanje u dvije faze. U prvoj fazi proces pokušava zaključati sve zapise koje treba, jednog po jednog. Ako uspije prelazi u drugu fazu, gdje ažurira zapise. Ako prilikom prve faze neki od zapisa nije mogao biti zakjučan u tom slučaju otpušta sve zaključane zapise i počinje ispočetka.

Osim problema sa potpunim zastojem, postoji i tzv. problem izgladnjivanja (eng. starvation), a to je problem da pojedini proces (s obzirom na neki način raspoređivanja) nikad ne dobije pravo izvršavanja, iako se sustav ne nalazi u stanju potpunog zastoja. Taj problem se obično rješava algoritmom raspoređivanja (npr. first-come, first-serve)

 

Zadatak: Odredite maksimalan broj operacija pri provjeri nekog stana bankarevim algoritmom ako se izvršava na n procesa i m tipova resursa.

 

Zadatak:.  Promotrimo sljedeći sustav gdje su U,V,W i X određeni tipovi resursa:

 

 

Alocirano

Maksimalno

Potražuje

Slobodno

U

V

W

X

U

V

W

X

U

V

W

X

U

V

W

X

A

0

0

1

2

0

0

1

2

0

0

0

0

1

5

2

0

B

1

0

0

0

1

7

5

0

0

7

5

0

C

1

3

5

4

2

3

5

6

1

0

0

2

D

0

6

3

2

0

6

5

2

0

0

2

0

E

0

0

1

4

0

6

5

6

0

6

4

2

 

Da li se ovaj sustav nalazi u sigurnom stanju?

Rješenje: Sljedeći koraci pokušavaju naći siguran niz. Kandidate za izvršavanje uvijek tražimo redom A,B,C,D,E.

 

Budući da je Slobodno = [1,5,2,0] veće ili jednako nego što su potrebe procesa A, možemo izvršiti A i nakon što završi slobodnim resursima pribrojiti resurse procesa A.

=> Slobodno = [1,5,2,0] + [0,0,1,2] = [1,5,3,2]

Sljedeći kojeg možemo izvršiti je C pa nakon njegovog izvršavanja

=> Slobodno = [1,5,3,2] + [1,3,5,4] = [2,8,8,6]

Sljedeći kojeg možemo izvršiti je B pa nakon njegovog izvršavanja

=> Slobodno = [2,8,8,6] + [1,0,0,0] = [3,8,8,6]

Sljedeći kojeg možemo izvršiti je D pa nakon njegovog izvršavanja

=> Slobodno = [3,8,8,6] + [0,6,3,2] = [3,14,11,8]

S obzirom da je [3,14,11,8] veće nego što E potražuje ( [0,6,4,2] ), možemo izvršiti E.

Na ovaj način smo pokazali da se gornjih pet procesa može izvršiti u redoslijedu A,C,B,D,E (tj. <A,C,B,D,E> je sigurna sekvenca) što pokazuje da je ovo stanje sigurno stanje.

 

 

Zadatak: Sustav raspolaže s 4 resursa (A, B, C, D) koji ima slijedeći broj instanci: A = 10, B = 11, C = 12, D = 13. Pretpostavimo da je u memoriji u nekom trenutku 5 procesa sa sljedećim alokacijama resursa i maksimalnim potrebama:

 

Proces

Alocirano

Maksimalno potrebno

 

A

B

C

D

A

B

C

D

1

2

1

2

4

a1

2

4

5

2

1

3

3

0

2

b2

7

2

3

3

1

2

3

3

2

c3

6

4

1

2

1

1

2

2

3

d4

5

2

2

1

0

a5

5

1

1

 

 

Utvrdite raspone vrijednosti za a1, b2, c3, d4 i a5 tako da se sustav nalazi u sigurnom stanju i niz procesa <p4, p2, p5, p3, p1> zadovoljava kriterij sigurnosti.

 

Rješenje: Zbog jednostavnosti formirajmo još vektor S (koji sadrži slobodne resurse) i matrciu P (koja sadrži broj resursa koji se potražuju po pojedinom procesu i pojedinom resursu). (... nastavak na papirima ...)

 



Zadatak: Sustav ima 4 procesa i 5 tipova resursa koji se mogu alocurati. Trenutno alocirane i maksimalne potrebe su:

 

 

Alocirano

Maksimum

Slobodno

A

1

0

2

1

1

1

1

2

1

3

0

0

X

1

1

B

2

0

1

1

0

2

2

2

1

0

C

1

1

0

1

0

2

1

3

1

0

D

1

1

1

1

0

1

1

2

2

1

 

 

Koja je najmanja vrijednost od x kako bi ovo stanje sustava bilo sigurno stanje?

 


[1] originalni u literaturi: preemptive – doslovni prevod bi bio pravno na kupnju iz prve ruke ili pretkupnja. Kod resursa se misli na slučaj da ako se jednom procesu dodijeli neki resurs da mu neki drugi proces ne može samo oduzeti taj resurs (primjer cd-pisač i memorija. Memoriju možemo privremeno oduzeti, lock na cd-pisaču ne)