Glasnik Matematicki, Vol. 54, No. 1 (2019), 21-52.
A POLYNOMIAL VARIANT OF A PROBLEM OF DIOPHANTUS AND ITS CONSEQUENCES
Alan Filipin and Ana Jurasić
Faculty of Civil Engineering, University of Zagreb, Fra Andrije Kačića-Miošića 26, 10 000 Zagreb, Croatia
e-mail: filipin@grad.hr
Department of Mathematics, University of Rijeka, Radmile Matejčić 2, 51 000 Rijeka, Croatia
e-mail: ajurasic@math.uniri.hr
Abstract.
In this paper we prove that every Diophantine quadruple in ℝ [X] is regular. In other words, we prove that if {a, b, c, d} is a set of four non-zero elements of ℝ[X], not all constant, such that the product of any two of its distinct elements increased by 1 is a square of an element of ℝ[X], then
(a+b-c-d)2=4(ab+1)(cd+1).
Some consequences of the above result are that for an arbitrary n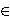 ℕ there does not exist a set of five non-zero elements from ℤ[X], which are not all constant, such that the product of any two of its distinct elements increased by n is a square of an element of ℤ[X]. Furthermore, there can exist such a set of four non-zero elements of ℤ[X] if and only if n is a square.
ℕ there does not exist a set of five non-zero elements from ℤ[X], which are not all constant, such that the product of any two of its distinct elements increased by n is a square of an element of ℤ[X]. Furthermore, there can exist such a set of four non-zero elements of ℤ[X] if and only if n is a square.
2010 Mathematics Subject Classification. 11D09,11D45
Key words and phrases. Diophantine m-tuples, polynomials
Full text (PDF) (free access)
https://doi.org/10.3336/gm.54.1.03
References:
-
J. Arkin, V. E. Hoggatt and E. G. Strauss, On Euler's solution of a problem of Diophantus,
Fibonacci Quart. 17 (1979), 333-339.
MathSciNet
-
A. Baker and H. Davenport, The equations 3x2 - 2 = y2 and
8x2 - 7 = z2, Quart. J. Math. Oxford Ser. (2) 20
(1969), 129-137.
MathSciNet
CrossRef
- E. Brown, Sets in which xy + k is always a square, Math. Comp. 45 (1985), 613-620.
MathSciNet
CrossRef
-
Y. Bugeaud, A. Dujella and M. Mignotte, On the family of
Diophantine triples {k - 1, k + 1, 16k3 - 4k}, Glasg. Math. J. 49 (2007), 333-344.
MathSciNet
CrossRef
- Diophantus of Alexandria, Arithmetics and the book
of polygonal numbers, (I. G. Bashmakova, Ed.) (Nauka 1974), 85-86,
215-217.
-
A. Dujella, Generalization of a problem of Diophantus, Acta Arith. 65 (1993), 15-27.
MathSciNet
CrossRef
- A. Dujella, The problem of the extension of a parametric
family of Diophantine triples, Publ. Math. Debrecen 51
(1997), 311-322.
MathSciNet
-
A. Dujella, On the exceptional set in the problem of Diophantus and Davenport, in: Application of Fibonacci Numbers, Vol. 7 eds. G. E. Bergum, A. N. Philippou, A. F. Horadam, Kluwer, Dordrecht, 1998, pp. 69-76.
MathSciNet
- A. Dujella, On the size of Diophantine m-tuples,
Math. Proc. Cambridge Philos. Soc. 132 (2002),
23-33.
MathSciNet
CrossRef
- A. Dujella, Bounds for the size of sets with the
property D(n), Glas. Mat. Ser. III 39 (2004),
199-205.
MathSciNet
CrossRef
- A. Dujella, There are only finitely many
Diophantine quintuples, J. Reine Angew. Math. 566 (2004), 183-214.
MathSciNet
CrossRef
- A. Dujella and C. Fuchs, A polynomial variant of a
problem of Diophantus and Euler, Rocky Mountain J. Math. 33 (2003), 797-811.
MathSciNet
CrossRef
- A. Dujella and C. Fuchs, Complete solution of the
polynomial version of a problem of Diophantus, J. Number
Theory 106 (2004), 326-344.
MathSciNet
CrossRef
- A. Dujella and C. Fuchs, On a problem of Diophantus for rationals, J. Number Theory 132 (2012), 2075-2083.
MathSciNet
CrossRef
- A. Dujella, C. Fuchs, F. Luca, A polynomial variant
of a problem of Diophantus for pure powers, Int. J. Number
Theory 4 (2008), 57-71.
MathSciNet
CrossRef
- A. Dujella, C. Fuchs and R. F. Tichy, Diophantine
m-tuples for linear polynomials, Period. Math. Hungar. 45 (2002), 21-33.
MathSciNet
CrossRef
- A. Dujella, C. Fuchs and G. Walsh, Diophantine
m-tuples for linear polynomials. II. Equal degrees, J. Number Theory, 120 (2006), 213-228.
MathSciNet
CrossRef
- A. Dujella and A. Jurasić, On the size of sets in a polynomial variant of a problem of
Diophantus, Int. J. Number Theory, 6 (2010), 1449-1471.
MathSciNet
CrossRef
- A. Dujella and M. Kazalicki, More on Diophantine sextuples, in: Number Theory - Diophantine problems, uniform distribution and applications, Festschrift in honour of Robert F. Tichy's 60th birthday, eds. C. Elsholtz, P. Grabner, Springer-Verlag, Berlin, 2017, 227-235.
MathSciNet
- A. Dujella, M. Kazalicki, M. Mikić and M. Szikszai, There are infinitely many rational Diophantine sextuples, Int. Math. Res. Not. IMRN 2017 (2) (2017), 490-508.
MathSciNet
CrossRef
- A. Dujella and F. Luca, On a problem of Diophantus
with polynomials, Rocky Mountain J. Math. 37
(2007), 131-157.
MathSciNet
CrossRef
- A. Dujella and A. Pethö, A generalization of a theorem of
Baker and Davenport, Quart. J. Math. Oxford Ser. (2) 49
(1998), 291-306.
MathSciNet
CrossRef
- A. Filipin and A. Jurasić, On the size of Diophantine m-tuples for linear polynomials, Miskolc Math. Notes, 17 (2016), 2; 861-876.
MathSciNet
CrossRef
-
Y. Fujita, The extensibility of Diophantine pairs {k-1,
k+1}, J. Number Theory 128 (2008), 322-353.
MathSciNet
CrossRef
- P. Gibbs, A generalised Stern-Brocot tree from
regular Diophantine quadruples. (Preprint).
math.NT/9903035.
- P. Gibbs, Some rational sextuples, Glas. Mat. Ser. III 41 (2006), 195-203.
MathSciNet
CrossRef
- B. He, A. Togbé and V. Ziegler, There is no Diophantine quintuple,
Trans. Amer. Math. Soc. 371 (2019), 6665-6709.
MathSciNet
CrossRef
- B. W. Jones, A second variation of a problem of
Davenport and Diophantus, Fibonacci Quart. 16
(1977), 155-165.
MathSciNet
- B. W. Jones, A variation of a problem of Davenport
and Diophantus, Quart. J. Math. Oxford Ser. (2) 27 (1976), 349-353.
MathSciNet
CrossRef
- A. Jurasić, Diophantine m-tuples
for quadratic polynomials, Glas. Mat. Ser. III, 46 (2011), 283-309.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
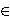 ℕ there does not exist a set of five non-zero elements from ℤ[X], which are not all constant, such that the product of any two of its distinct elements increased by n is a square of an element of ℤ[X]. Furthermore, there can exist such a set of four non-zero elements of ℤ[X] if and only if n is a square.
ℕ there does not exist a set of five non-zero elements from ℤ[X], which are not all constant, such that the product of any two of its distinct elements increased by n is a square of an element of ℤ[X]. Furthermore, there can exist such a set of four non-zero elements of ℤ[X] if and only if n is a square.