Glasnik Matematicki, Vol. 53, No. 2 (2018), 239-264.
ON POINCARÉ SERIES OF HALF-INTEGRAL WEIGHT
Sonja Žunar
Department of Mathematics,
Faculty of Science,
University of Zagreb,
Bijenička 30, 10000 Zagreb,
Croatia
e-mail: szunar@math.hr
Abstract.
We use Poincaré series of K -finite matrix coefficients of genuine integrable representations of the metaplectic cover of SL2(ℝ) to construct a spanning set for the space of cusp forms Sm(Γ,χ) , where Γ is a discrete subgroup of finite covolume in the metaplectic cover of SL2(ℝ) , χ is a character of Γ of finite order, and m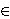 5/2+ℤ≥0 . We give a result on the non-vanishing of the constructed cusp forms and compute their Petersson inner product with any f
5/2+ℤ≥0 . We give a result on the non-vanishing of the constructed cusp forms and compute their Petersson inner product with any f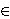 Sm(Γ,χ) . Using this last result, we construct a Poincaré series ΔΓ,k,m,ξ,χ
Sm(Γ,χ) . Using this last result, we construct a Poincaré series ΔΓ,k,m,ξ,χ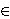 Sm(Γ,χ) that corresponds, in the sense of the Riesz representation theorem, to the linear functional f ↦ f(k)(ξ) on Sm(Γ,χ) , where ξ
Sm(Γ,χ) that corresponds, in the sense of the Riesz representation theorem, to the linear functional f ↦ f(k)(ξ) on Sm(Γ,χ) , where ξ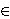 ℂℑ(z)>0 and k
ℂℑ(z)>0 and k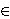 ℤ≥0 . Under some additional conditions on Γ and χ , we provide the Fourier expansion of cusp forms ΔΓ,k,m,ξ,χ and their expansion in a series of classical Poincaré series.
ℤ≥0 . Under some additional conditions on Γ and χ , we provide the Fourier expansion of cusp forms ΔΓ,k,m,ξ,χ and their expansion in a series of classical Poincaré series.
2010 Mathematics Subject Classification. 11F12, 11F37
Key words and phrases. Cusp forms of half-integral weight, Poincaré series, metaplectic cover of SL2(ℝ)
Full text (PDF) (free access)
DOI: 10.3336/gm.53.2.03
References:
- Harish-Chandra, Discrete series for semisimple Lie groups II. Explicit determination of the characters, Acta Math. 116 (1966), 1-111.
MathSciNet
CrossRef
- A. W. Knapp and D. A. Vogan, Jr., Cohomological induction and unitary representations, Princeton University Press, Princeton, 1995.
MathSciNet
CrossRef
- N. Koblitz, Introduction to elliptic curves and modular forms, Springer, New York, 2nd ed., 1993.
MathSciNet
CrossRef
- T. Miyake, Modular forms, Springer, Berlin, 2006.
MathSciNet
- G. Muić, On the cuspidal modular forms for the Fuchsian groups of the first kind, J. Number Theory 130 (2010), 1488-1511.
MathSciNet
CrossRef
- G. Muić, Modular curves and bases for the spaces of cuspidal modular forms, Ramanujan J. 27 (2012), 181-208.
MathSciNet
CrossRef
- G. Muić, On the analytic continuation and non-vanishing of L-functions, Int. J. Number Theory 8 (2012), 1831-1854.
MathSciNet
CrossRef
- G. Muić, On the non-vanishing of certain modular forms, Int. J. Number Theory 7 (2011), 351-370.
MathSciNet
CrossRef
- G. Muić, On the inner product of certain automorphic forms and applications, J. Lie Theory 22 (2012), 1091-1107.
MathSciNet
- R Core Team, R: A language and environment for statistical computing. R Foundation for statistical computing, Vienna, Austria, 2016. https://www.R-project.org/.
- G. Shimura, On modular forms of half integral weight, Ann. of Math. (2) 97 (1973), 440-481.
MathSciNet
CrossRef
- S. Žunar, On the non-vanishing of Poincaré series on the metaplectic group, to appear in Manuscripta Math. (2018). https://doi.org/10.1007/s00229-018-1011-6.
Glasnik Matematicki Home Page
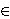 5/2+ℤ≥0 . We give a result on the non-vanishing of the constructed cusp forms and compute their Petersson inner product with any f
5/2+ℤ≥0 . We give a result on the non-vanishing of the constructed cusp forms and compute their Petersson inner product with any f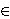 Sm(Γ,χ) . Using this last result, we construct a Poincaré series ΔΓ,k,m,ξ,χ
Sm(Γ,χ) . Using this last result, we construct a Poincaré series ΔΓ,k,m,ξ,χ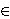 Sm(Γ,χ) that corresponds, in the sense of the Riesz representation theorem, to the linear functional f ↦ f(k)(ξ) on Sm(Γ,χ) , where ξ
Sm(Γ,χ) that corresponds, in the sense of the Riesz representation theorem, to the linear functional f ↦ f(k)(ξ) on Sm(Γ,χ) , where ξ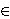 ℂℑ(z)>0 and k
ℂℑ(z)>0 and k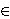 ℤ≥0 . Under some additional conditions on Γ and χ , we provide the Fourier expansion of cusp forms ΔΓ,k,m,ξ,χ and their expansion in a series of classical Poincaré series.
ℤ≥0 . Under some additional conditions on Γ and χ , we provide the Fourier expansion of cusp forms ΔΓ,k,m,ξ,χ and their expansion in a series of classical Poincaré series.