Glasnik Matematicki, Vol. 53, No. 2 (2018), 229-238.
TOTALLY REAL THUE INEQUALITIES OVER IMAGINARY QUADRATIC FIELDS
István Gaál, Borka Jadrijević and László Remete
University of Debrecen, Mathematical Institute,
H-4002 Debrecen Pf.400., Hungary
e-mail: gaal.istvan@unideb.hu
University of Split, Faculty of Science,
Rudjera Boškovića 33, 21000 Split, Croatia
e-mail: borka@pmfst.hr
University of Debrecen, Mathematical Institute,
H-4002 Debrecen Pf.400., Hungary
e-mail: remete.laszlo@science.unideb.hu
Abstract.
Let F(x,y) be an irreducible binary form of degree ≥ 3 with
integer coefficients and with real roots. Let M be an imaginary quadratic field
with ring of integers ℤM. Let K>0.
We describe an efficient method how to reduce the resolution of the relative Thue
inequalities
|F(x,y)|≤ K (x,y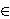 ℤM)
to the resolution of absolute Thue inequalities of type
|F(x,y)|≤ k (x,y
ℤM)
to the resolution of absolute Thue inequalities of type
|F(x,y)|≤ k (x,y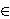 ℤ).
We illustrate our method with an explicit example.
ℤ).
We illustrate our method with an explicit example.
2010 Mathematics Subject Classification. 11D59, 11D57
Key words and phrases. Relative Thue equations, Thue inequalities
Full text (PDF) (free access)
DOI: 10.3336/gm.53.2.02
References:
-
A. Baker, Transcendental number theory, Cambridge University Press, Cambridge, 1990.
MathSciNet
-
W. Bosma, J. Cannon and C. Playoust,
The Magma algebra system.I. The user language,
J. Symbolic Comput. 24 (1997), 235-265.
MathSciNet
CrossRef
-
B. W. Char, K. O. Geddes, G. H. Gonnet, M. B. Monagan, S. M. Watt,
MAPLE, Reference Manual, Watcom Publications, Waterloo, Canada, 1988.
-
M. Daberkow, C. Fieker, J. Klüners, M. Pohst, K.Roegner and K. Wildanger, KANT V4, Computational algebra and number theory, J. Symbolic Comput. 24 (1997), 267-283. http://www.math.tu-berlin.de/~kant/.
MathSciNet
CrossRef
-
I. Gaál,
Computing elements of given index in totally complex cyclic
sextic fields,
J. Symbolic Comput. 20 (1995), 61-69.
MathSciNet
CrossRef
-
I. Gaál, Diophantine equations and power integral bases,
Birkhäuser, Boston, 2002.
MathSciNet
-
I. Gaál and M. Pohst, On the resolution of relative Thue equations, Math. Comput. 71 (2002), 429-440.
MathSciNet
CrossRef
-
S. V. Kotov and V. G. Sprindžuk, An effective analysis of the Thue-Mahler equation in relative fields (Russian),
Dokl. Akad. Nauk. BSSR 17 (1973), 393-395, 477.
MathSciNet
-
A. Pethő, On the resolution of Thue inequalities,
J. Symbolic Comput. 4 (1987), 103-109.
MathSciNet
CrossRef
-
A. Thue, Über Annäherungswerte algebraischer Zahlen,
J. Reine Angew. Math. 135 (1909), 284-305.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
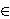 ℤM)
ℤM)
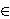 ℤM)
ℤM)
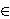 ℤ).
ℤ).