Glasnik Matematicki, Vol. 53, No. 1 (2018), 73-95.
A RESULT IN THE SPIRIT OF HERSTEIN THEOREM
Maja Fošner, Benjamin Marcen and Joso Vukman
Faculty of logistics, University of Maribor, Mariborska cesta 7, 3000 Celje, Slovenia
e-mail: maja.fosner@um.si
Faculty of logistics, University of Maribor, Mariborska cesta 7, 3000 Celje, Slovenia
e-mail: benjamin.marcen@um.si
Institute of mathematics, physics and mechanics, Jadranska 19, 1000 Ljubljana, Slovenia
e-mail: joso.vukman@guest.um.si
Abstract.
A classical result of Herstein asserts that any Jordan
derivation on a prime ring of characteristic different from two is a derivation.
It is our aim in this paper to prove the following result,
which is in the spirit of Herstein's theorem.
Let n≥ 3 be some fixed integer, let R be a prime ring with char(R)> 4n-8 and let D:R → R be an additive mapping satisfying either the
relation D(xn)=D(xn-1)x+xn-1D(x) or the relation D(xn)=D(x)xn-1+xD(xn-1) for all x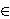 R. In both cases D is a derivation.
R. In both cases D is a derivation.
2010 Mathematics Subject Classification.
16W10, 39B05.
Key words and phrases. Prime ring, semiprime ring, derivation,
Jordan derivation, functional identity.
Full text (PDF) (free access)
DOI: 10.3336/gm.53.1.06
References:
- K. I. Beidar, M. Brešar, M. A. Chebotar and W. S.
Martindale 3rd, On Herstein's Lie map conjectures II, J. Algebra
238 (2001), 239-264.
MathSciNet
CrossRef
- K. I. Beidar and Y. Fong, On additive isomorphisms of prime
rings preserving polynomials, J. Algebra 217 (1999), 650-667.
MathSciNet
CrossRef
- M. Brešar, Jordan derivations on semiprime rings,
Proc. Amer. Math. Soc. 104 (1988), 1003-1006.
MathSciNet
CrossRef
- M. Brešar, Jordan mappings of semiprime rings, J.
Algebra 127 (1989), 218-228.
MathSciNet
CrossRef
- M. Brešar, Functional identities: A survey, in: Algebra and its applications,
Contemp. Math. 259, Amer. Math. Soc., Providence, 2000, 93-109.
- M. Brešar, M. Chebotar and W. S. Martindale 3rd,
Functional identities, Birkhäuser Verlag, Basel, 2007.
MathSciNet
- M. Brešar and J. Vukman, Jordan derivations on prime
rings, Bull. Austral. Math. Soc. 37 (1988), 321-322.
MathSciNet
CrossRef
- M. Brešar and J. Vukman, Jordan (θ ,φ )-derivations, Glas. Mat. Ser. III 26(46) (1991), 13-17.
MathSciNet
- Cheng-Kai Liu and Wen-Kwei Shiue, Generalized Jordan triple
(θ ,φ )-derivations on semiprime rings, Taiwanese J. Math.
11 (2007), 1397-1406.
MathSciNet
CrossRef
- J. M. Cusack, Jordan derivations on rings, Proc. Amer.
Math. Soc. 53 (1975), 321-324.
MathSciNet
CrossRef
- M. Fošner and N. Peršin, A result concerning derivations in prime rings, Glas. Mat. Ser. III 48(68) (2013), 67-79.
MathSciNet
CrossRef
- I. N. Herstein, Jordan derivations of prime rings, Proc.
Amer. Math. Soc. 8 (1957), 1104-1110.
MathSciNet
CrossRef
- L. Rowen, Some results on the center of a ring with polynomial identity, Bull. Amer. Math. Soc. 79 (1973), 219-223.
MathSciNet
CrossRef
- J. Vukman, On derivations of standard operator algebras
and semisimple H* -algebras, Studia Sci. Math. Hungar. 44
(2007), 57-63.
MathSciNet
CrossRef
- J. Vukman, Some remarks on derivations in semiprime
rings and standard operator algebras, Glas. Mat. Ser. III 46(66) (2011), 43-48.
MathSciNet
CrossRef
- J. Vukman, I. Kosi-Ulbl and D. Eremita, On certain equations
in rings, Bull. Austral. Math. Soc. 71 (2005), 53-60.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
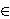 R. In both cases D is a derivation.
R. In both cases D is a derivation.
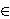 R. In both cases D is a derivation.
R. In both cases D is a derivation.