Glasnik Matematicki, Vol. 52, No. 2 (2017), 377-410.
LOCAL ASYMPTOTIC MIXED NORMALITY OF APPROXIMATE MAXIMUM LIKELIHOOD ESTIMATOR OF DRIFT PARAMETERS IN DIFFUSION MODEL
Snježana Lubura Strunjak and Miljenko Huzak
Department of Mathematics, Faculty of Science, University of Zagreb,
Bijenička 30, 10 000 Zagreb, Croatia
e-mail: snjezana.lubura.strunjak@math.hr
e-mail: miljenko.huzak@math.hr
Abstract.
We assume that the diffusion X satisfies a stochastic differential equation of the form:
dXt=μ(Xt,θ)dt+σ0ν(Xt)dWt, with unknown drift parameter θ and known diffusion coefficient parameter σ0. We prove that approximate maximum likelihood estimator of drift parameter θ n obtained from discrete
observations (XiΔn,0≤ i≤ n) along fixed time interval [0,T], and when Δn =T/n tends to zero, is locally asymptotic mixed normal, with covariance matrix which depends on MLE 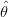 obtained from continuous observations (Xt,0≤ t≤ T) along fixed time interval [0,T], and on path (Xt,0≤ t≤ T).
obtained from continuous observations (Xt,0≤ t≤ T) along fixed time interval [0,T], and on path (Xt,0≤ t≤ T).
2010 Mathematics Subject Classification.
62M05, 62F12, 60J60.
Key words and phrases. Asymptotic mixed normality, diffusion processes, discrete observation, parameter estimation.
Full text (PDF) (free access)
DOI: 10.3336/gm.52.2.13
References:
- D. J. Aldous and G. K. Eagleson, On mixing and stability of limit theorems, Ann. Probability 6 (1978) 325-331.
MathSciNet
CrossRef
- P. Billingsley, Convergence of probability measures, 2nd edn. Wiley and Sons, New York,
1999.
MathSciNet
- B. M. Brown and J. I. Hewitt, Asymptotic likelihood theory for diffusion processes,
J. Appl. Probab. 12 (1975), 228-238.
MathSciNet
CrossRef
- D. Dacunha-Castelle and D. Florens-Zmirou, Estimation of the coefficients of a diffusion from discrete observations,
Stochastics 19 (1986), 263-284.
MathSciNet
CrossRef
- P. D. Feigin, Maximum likelihood estimation for continuous-time stochastic processes
Adv. in Appl. Probab. 8 (1976), 712-736.
MathSciNet
CrossRef
- D. Florens-Zmirou, Approximate discrete time shemes for statistics of diffusion processes, Statistics 20 (1989), 547-557.
MathSciNet
CrossRef
- M. Huzak, Selection of diffusion growth process and parameter estimation from discrete observation, Ph.D. thesis,
University of Zagreb, (in Croatian), 1997.
- M. Huzak, Parameter estimation of diffusion models, Math. Commun. 3 (1998), 129-134.
MathSciNet
- M. Huzak, A general theorem on approximate maximum likelihood estimation, Glas. Mat. Ser. III 36(56) (2001), 139-153.
MathSciNet
- M. Huzak, Estimating a class of diffusions from discrete observations via approximate
maximum likelihood method, Statistics, to appear.
- J. Jacod, On continuous conditional Gaussian martingales and stable convergence in law, in: Séminaire de probabilitiés (Strasbourg), XXXI, Lecture Notes in Math. 1655, Springer, Berlin, 1997, 232-246.
MathSciNet
- J. Jacod and P. Protter, Discretization of processes, Springer, Heidelberg, 2012.
MathSciNet
- J. Jacod and A. N. Shiryaev, Limit theorems for stochastic processes, Springer-Verlag, Berlin, 2003.
MathSciNet
- M. Kessler, Estimation of an Ergodic Diffusion from Discrete Observations, Scand. J. Statist. 24 (1997), 211-229.
MathSciNet
CrossRef
- A. LeBreton, On continuous and discrete sampling for parameter estimation in diffusion type
processes, Math. Programming Stud. 5 (1976), 124-144.
MathSciNet
CrossRef
- R. S. Liptser and A. N. Shiryaev, Statistics of random processes II. Applications, Springer-Verlag, New York-Heidelberg, 1978.
MathSciNet
- P. Protter (2004). Stochastic integration and differential equations, Springer-Verlag, Berlin, 2004.
MathSciNet
- A. Rényi, On stable sequences of events, Sankhya Ser. A 25 (1963), 293-302.
MathSciNet
- D. Revuz and M. Yor, Continuous martingales and Brownian motion, Springer-Verlag, Berlin, 1999.
MathSciNet
- L. C. G. Rogers and D. Williams, Diffusion, Markov processes, and martingales, Vol. 2.
Itô calculus. John Wiley & Sons, Ltd., New York, 1987.
MathSciNet
Glasnik Matematicki Home Page
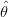 obtained from continuous observations (Xt,0≤ t≤ T) along fixed time interval [0,T], and on path (Xt,0≤ t≤ T).
obtained from continuous observations (Xt,0≤ t≤ T) along fixed time interval [0,T], and on path (Xt,0≤ t≤ T).
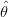 obtained from continuous observations (Xt,0≤ t≤ T) along fixed time interval [0,T], and on path (Xt,0≤ t≤ T).
obtained from continuous observations (Xt,0≤ t≤ T) along fixed time interval [0,T], and on path (Xt,0≤ t≤ T).