Glasnik Matematicki, Vol. 52, No. 1 (2017), 79-98.
QUASI-PARTICLE BASES OF PRINCIPAL SUBSPACES OF THE AFFINE LIE ALGEBRA OF TYPE G2(1)
Marijana Butorac
Department of Mathematics, University of Rijeka, Radmile Matejčić 2, 51 000 Rijeka, Croatia
e-mail: mbutorac@math.uniri.hr
Abstract.
The aim of this work is to construct the quasi-particle basis of principal subspace of standard module of highest weight kΛ0 of level k≥ 1 of affine Lie algebra of type G2(1) by means of which we obtain the basis of principal subspace of generalized Verma module.
2010 Mathematics Subject Classification.
17B67, 17B69, 05A19.
Key words and phrases. Affine Lie algebras, vertex operator algebras, principal subspaces, quasi-particle bases.
Full text (PDF) (free access)
DOI: 10.3336/gm.52.1.06
References:
- G. E. Andrews, The theory of partitions, Encyclopedia
of Mathematics and Its Applications, Vol. 2, Addison-Wesley, 1976.
MathSciNet
- G. E. Andrews, Partitions and Durfee dissection, Amer. J. Math. 101 (1979), 735-742.
MathSciNet
CrossRef
- E. Ardonne, R. Kedem and M. Stone, Fermionic characters and arbitrary highest-weight integrable
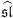 r+1-modules, Comm. Math. Phys. 264 (2006), 427-464.
r+1-modules, Comm. Math. Phys. 264 (2006), 427-464.
MathSciNet
CrossRef
- M. Butorac, Combinatorial bases of principal subspaces for the affine Lie algebra of type B2(1), J. Pure Appl. Algebra 218 (2014), 424-447.
MathSciNet
CrossRef
- M. Butorac, Quasi-particle bases of principal subspaces for the affine Lie algebras of type Bl(1) and Cl(1), Glas. Mat. Ser. III 51(71) (2016), 59-108.
MathSciNet
CrossRef
- C. Calinescu, Intertwining vertex operators and certain representations of
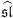 (n),
Commun. Contemp. Math. 10 (2008), 47-79.
(n),
Commun. Contemp. Math. 10 (2008), 47-79.
MathSciNet
CrossRef
- C. Calinescu, Principal subspaces of higher-level standard
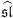 (3)-modules, J. Pure
Appl. Algebra 210 (2007), 559-575.
(3)-modules, J. Pure
Appl. Algebra 210 (2007), 559-575.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of
certain A(1)1-modules, I. Level one case, Internat. J. Math. 19 (2008), 71-92.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of
certain A(1)1 -modules, II. Higher-level case, J. Pure Appl. Algebra 212 (2008), 1928-1950.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of the principal subspaces of
level one modules for the untwisted affine Lie algebras of types A, D, E, J. Algebra 323 (2010), 167-192.
MathSciNet
CrossRef
- C. Calinescu, J. Lepowsky and A. Milas, Vertex-algebraic structure of principal subspaces of
standard A2(2)-modules, I, Internat. J. Math. 25 (2014), 1450063, 44 pp.
MathSciNet
CrossRef
- C. Calinescu, A. Milas and M. Penn, Vertex algebraic structure of principal subspaces of basic A2n(2)-modules, J. Pure Appl. Algebra 220 (2016), 1752-1784.
MathSciNet
CrossRef
- S. Capparelli, J. Lepowsky and A. Milas, The Rogers-Ramanujan recursion and
intertwining operators, Commun. Contemp. Math. 5 (2003), 947-966.
MathSciNet
CrossRef
- S. Capparelli, J. Lepowsky and A. Milas, The Rogers-Selberg recursions, the Gordon-Andrews
identities and intertwining operators, Ramanujan J. 12 (2006), 379-397.
MathSciNet
CrossRef
- E. Feigin, The PBW filtration, Represent. Theory 13 (2009), 165-181.
MathSciNet
CrossRef
- B. L. Feigin and A. V. Stoyanovsky, Functional models of the representations of
current algebras, and semi-infinite Schubert cells, (Russian) Funktsional. Anal. i
Prilozhen. 28 (1994), 68-90, 96; translation in Funct. Anal. Appl. 28 (1994),
55-72.
MathSciNet
CrossRef
- I. B. Frenkel, Y.-Z. Huang and J. Lepowsky,
On axiomatic approaches to vertex operator algebras and modules, Memoirs of the Amer. Math. Soc. 104, (1993), no. 494, 64 pp.
MathSciNet
CrossRef
- G. Georgiev, Combinatorial constructions of modules for infinite-dimensional Lie algebras,
I. Principal subspace, J. Pure Appl. Algebra 112 (1996), 247-286.
MathSciNet
CrossRef
- D. Gepner, New conformal theories associated with Lie algebras and their partition functions, Nuclear Phys. B 290 (1987), 10-24.
MathSciNet
CrossRef
- M. Jerković and M. Primc, Quasi-particle fermionic formulas for (k, 3)-admissible configurations, Cent. Eur. J. Math. 10 (2012), 703-721.
MathSciNet
CrossRef
- V. G. Kac, Infinite dimensional Lie algebras, 3rd ed., Cambridge University Press, Cambridge,
1990.
MathSciNet
CrossRef
- S. Kožić, Principal subspaces for quantum affine algebra Uq(A(1)n), J. Pure Appl. Algebra 218 (2014), 2119-2148.
MathSciNet
CrossRef
- S. Kožić, Vertex operators and principal subspaces of level one for Uq(
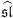 2), J. Algebra 455 (2016), 251-290.
2), J. Algebra 455 (2016), 251-290.
MathSciNet
CrossRef
- S. Kožić and M. Primc, Quasi-particles in the principal picture of
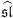 2 and Rogers-Ramanujan-type identities, preprint.
2 and Rogers-Ramanujan-type identities, preprint.
- J. Lepowsky and H.-S. Li, Introduction to vertex operator algebras and
their representations, Birkhäuser, Boston, 2003.
MathSciNet
CrossRef
- J. Lepowsky and M. Primc, Standard modules for type one affine Lie algebras, Lecture Notes in
Math. 1052 (1984), 194-251.
MathSciNet
CrossRef
- A. Meurman and M. Primc, Annihilating fields of standard modules
of
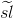 (2, C) and combinatorial identities, Mem. Amer. Math. Soc. 137 (1999), no. 652, 89pp.
(2, C) and combinatorial identities, Mem. Amer. Math. Soc. 137 (1999), no. 652, 89pp.
MathSciNet
CrossRef
- M. Penn and C. Sadowski, Vertex-algebraic structure of principal subspaces of basic D(3)4-modules, The Ramanujan Journal, to appear.
- M. Penn and C. Sadowski, Vertex-algebraic structure of principal subspaces of basic modules for twisted affine Kac-Moody Lie algebras of type A2n+1(2), Dn(2), E6(2), preprint.
- C. Sadowski, Presentations of the principal subspaces of the higher-level standard
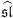 (3)-modules, J. Pure Appl. Algebra 219 (2015), 2300-2345.
(3)-modules, J. Pure Appl. Algebra 219 (2015), 2300-2345.
MathSciNet
CrossRef
- C. Sadowski, Principal subspaces of higher-level standard
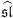 (n)-modules, Int. J. Math. 26 (2015), 1550053, 35 pp.
(n)-modules, Int. J. Math. 26 (2015), 1550053, 35 pp.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
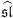 r+1-modules, Comm. Math. Phys. 264 (2006), 427-464.
r+1-modules, Comm. Math. Phys. 264 (2006), 427-464.
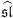 (n),
Commun. Contemp. Math. 10 (2008), 47-79.
(n),
Commun. Contemp. Math. 10 (2008), 47-79.
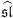 (3)-modules, J. Pure
Appl. Algebra 210 (2007), 559-575.
(3)-modules, J. Pure
Appl. Algebra 210 (2007), 559-575.
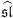 2), J. Algebra 455 (2016), 251-290.
2), J. Algebra 455 (2016), 251-290.
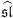 2 and Rogers-Ramanujan-type identities, preprint.
2 and Rogers-Ramanujan-type identities, preprint.
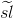 (2, C) and combinatorial identities, Mem. Amer. Math. Soc. 137 (1999), no. 652, 89pp.
(2, C) and combinatorial identities, Mem. Amer. Math. Soc. 137 (1999), no. 652, 89pp.
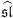 (3)-modules, J. Pure Appl. Algebra 219 (2015), 2300-2345.
(3)-modules, J. Pure Appl. Algebra 219 (2015), 2300-2345.
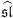 (n)-modules, Int. J. Math. 26 (2015), 1550053, 35 pp.
(n)-modules, Int. J. Math. 26 (2015), 1550053, 35 pp.