Glasnik Matematicki, Vol. 52, No. 1 (2017), 45-52.
ON SEQUENCES OF CONSECUTIVE SQUARES ON ELLIPTIC CURVES
Mohamed Kamel and Mohammad Sadek
Department of Mathematics, Faculty of Science, Cairo University, Giza, Egypt
e-mail: mohgamal@sci.cu.edu.eg
Mathematics and Actuarial Science Department, American University in Cairo, AUC Avenue, New Cairo, Egypt
e-mail: mmsadek@aucegypt.edu
Abstract.
Let C be an elliptic curve defined over Q by the equation y2=x3+Ax+B where A,B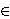 Q. A sequence of rational points (xi,yi)
Q. A sequence of rational points (xi,yi)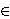 C(Q), i=1,2,…, is said to form a sequence of consecutive squares on C if the sequence of x-coordinates, xi,i=1,2,…, consists of consecutive squares. We produce an infinite family of elliptic curves C with a 5-term sequence of consecutive squares. Furthermore, this sequence consists of five independent rational points in C(Q). In particular, the rank r of C(Q) satisfies r≥ 5.
C(Q), i=1,2,…, is said to form a sequence of consecutive squares on C if the sequence of x-coordinates, xi,i=1,2,…, consists of consecutive squares. We produce an infinite family of elliptic curves C with a 5-term sequence of consecutive squares. Furthermore, this sequence consists of five independent rational points in C(Q). In particular, the rank r of C(Q) satisfies r≥ 5.
2010 Mathematics Subject Classification.
14G05, 11B83.
Key words and phrases. Elliptic curves, rational points, sequences of consecutive squares.
Full text (PDF) (free access)
DOI: 10.3336/gm.52.1.04
References:
-
A. Alvarado,
An arithmetic progression on quintic curves,
J. Integer Seq. 12 (2009),
Article 09.7.3, 6pp.
MathSciNet
- W. Bosma and J. Cannon and C. Playoust, The Magma algebra system. I. The user language,
J. Symbolic Comput. 24 (1997), 235-265.
MathSciNet
CrossRef
- A. Bremner,
On arithmetic progressions on elliptic curves,
Exp. Math. 8 (1999), 409-413.
MathSciNet
CrossRef
- A. Bremner and M. Ulas,
Rational points in geometric progressions on certain hyperelliptic curves,
Publ. Math. Debrecen 82 (2013), 669-683.
MathSciNet
CrossRef
- G. Campbell,
A note on arithmetic progressions on elliptic curves,
J. Integer Seq. 6 (2003), Article 03.1.3, 5pp.
MathSciNet
-
G. Faltings,
Endlichkeitssätze für abelsche Varietäten über Zahlkörpern,
Invent. Math. 73 (1983), 349-366.
MathSciNet
CrossRef
-
A. J. MacLeod,
14-term arithmetic progressions on quartic elliptic curves,
J. Integer Seq. 9 (2006), Article 06.1.2, 4pp.
MathSciNet
-
L. J. Mordell, Diophantine Equations, Academic Press, New York, 1969.
MathSciNet
-
M. Stoll and J. E. Cremona,
Minimal models for 2-coverings of elliptic curve,
LMS J. Comput. Math. 5 (2002), 220-243.
MathSciNet
CrossRef
-
M. Ulas,
A note on arithmetic progressions on quartic elliptic curves,
J. Integer Seq. 8 (2005), Article 05.3.1, 5pp.
MathSciNet
Glasnik Matematicki Home Page
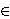 Q. A sequence of rational points (xi,yi)
Q. A sequence of rational points (xi,yi)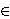 C(Q), i=1,2,…, is said to form a sequence of consecutive squares on C if the sequence of x-coordinates, xi,i=1,2,…, consists of consecutive squares. We produce an infinite family of elliptic curves C with a 5-term sequence of consecutive squares. Furthermore, this sequence consists of five independent rational points in C(Q). In particular, the rank r of C(Q) satisfies r≥ 5.
C(Q), i=1,2,…, is said to form a sequence of consecutive squares on C if the sequence of x-coordinates, xi,i=1,2,…, consists of consecutive squares. We produce an infinite family of elliptic curves C with a 5-term sequence of consecutive squares. Furthermore, this sequence consists of five independent rational points in C(Q). In particular, the rank r of C(Q) satisfies r≥ 5.