Glasnik Matematicki, Vol. 51, No. 2 (2016), 453-474.
DYNAMIC PROPERTIES FOR THE INDUCED MAPS ON n-FOLD SYMMETRIC PRODUCT SUSPENSIONS
Franco Barragán, Alicia Santiago-Santos and Jesús F. Tenorio
Instituto de Física y Matemáticas,
Universidad Tecnológica de la Mixteca, Carretera a Acatlima, Km. 2.5, Huajuapan de León, Oaxaca, C.P. 69000, México
e-mail: franco@mixteco.utm.mx
e-mail: alicia@mixteco.utm.mx
e-mail: jtenorio@mixteco.utm.mx
Abstract.
Let X be a continuum. For any positive integer n we consider the hyperspace Fn(X) and if n is greater than or equal to two, we consider the quotient space SFn(X)
defined in [3]. For a given map f:X → X, we consider the induced maps Fn(f): Fn(X) → Fn(X) and SFn(f): SFn(X) → SFn(X) defined in
[4]. Let M be one of the following classes of maps: exact, mixing, weakly mixing, transitive, totally transitive, strongly transitive, chaotic, minimal, irreducible, feebly open and turbulent.
In this paper we study the relationships between the following statements: f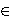 M, Fn(f)
M, Fn(f)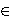 M and SFn(f)
M and SFn(f)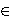 M.
M.
2010 Mathematics Subject Classification.
54B20, 37B45, 54F50, 54F15.
Key words and phrases. Chaotic map, exact map, feebly open map, hyperspace, induced map, irreducible map, minimal map, mixing map, strongly transitive map, symmetric product, symmetric product suspension, totally transitive map, transitive map, turbulent map,
weakly mixing map.
Full text (PDF) (free access)
DOI: 10.3336/gm.51.2.12
References:
- G. Acosta, A. Illanes and H. Méndez-Lango,
The transitivity of induced maps,
Topology Appl. 156 (2009), 1013-1033.
MathSciNet
CrossRef
- J. Banks,
Chaos for induced hyperspace maps,
Chaos Solitons Fractals 25 (2005), 681-685.
MathSciNet
CrossRef
- F. Barragán,
On the n-fold symmetric product suspensions of a continuum,
Topology Appl. 157 (2010), 597-604.
MathSciNet
CrossRef
- F. Barragán,
Induced maps on n-fold symmetric product suspensions,
Topology Appl. 158 (2011), 1192-1205.
MathSciNet
CrossRef
- F. Barragán,
Aposyndetic properties of the n-fold symmetric product suspensions
of a continuum,
Glas. Mat. Ser. III 49(69) (2014), 179-193.
MathSciNet
CrossRef
- F. Barragán, S. Macías and J. F. Tenorio,
More on induced maps on n-fold symmetric product suspensions,
Glas. Mat. Ser. III 50(70) (2015), 489-512.
MathSciNet
CrossRef
- J. Camargo, C. García and A. Ramírez,
Transitivity of the induced map Cn(f),
Rev. Colombiana Mat. 48 (2014), 235-245.
MathSciNet
CrossRef
- J. S. Cánovas-Peña and G. S. López,
Topological entropy for induced hyperspace maps,
Chaos Solitons Fractals 28 (2006), 979-982.
MathSciNet
CrossRef
- J. Dugundji,
Topology, Allyn and Bacon, Inc., Boston, 1966.
MathSciNet
- J. L. Gómez-Rueda, A. Illanes and H. Méndez-Lango,
Dynamic properties for the induced maps in the symmetric products,
Chaos Solitons Fractals 45 (2012), 1180-1187.
MathSciNet
CrossRef
- G. Higuera and A. Illanes,
Induced mappings on symmetric products,
Topology Proc. 37 (2011), 367-401.
MathSciNet
- R. Gu and W. Guo,
On mixing property in set-valued discrete systems,
Chaos Solitons Fractals 28 (2006), 747-754.
MathSciNet
CrossRef
- A. Illanes and S. B. Nadler, Jr.,
Hyperspaces. Fundamentals and recent advances, Marcel Dekker, New York, 1999.
MathSciNet
- S. Kolyada, L. Snoha and S. Trofimchuk,
Noninvertible minimal maps,
Fund. Math. 168 (2001), 141-163.
MathSciNet
CrossRef
- D. Kwietniak and M. Misiurewicz,
Exact Devaney chaos and entropy,
Qual. Theory Dyn. Syst. 6 (2005), 169-179.
MathSciNet
CrossRef
- X. Ma, B. Hou and G. Liao,
Chaos in hyperspace system,
Chaos Solitons Fractals 40 (2009), 653-660.
MathSciNet
CrossRef
- S. Macías,
Topics on continua, Chapman & Hall/CRC, Boca Raton, 2005.
MathSciNet
CrossRef
- S. B. Nadler, Jr.,
Hyperspaces of sets, Marcel Dekker, New York-Basel, 1978. Reprinted by: Sociedad Matemática Mexicana, México, 2006.
MathSciNet
MathSciNet
- S. B. Nadler, Jr.,
Continuum theory. An introduction, Marcel Dekker, New York, 1992.
MathSciNet
- A. Peris,
Set-valued discrete chaos,
Chaos Solitons Fractals 26 (2005), 19-23.
MathSciNet
CrossRef
- H. Román-Flores,
A note on transitivity in set-valued discrete systems,
Chaos Solitons Fractals 17 (2003), 99-104.
MathSciNet
CrossRef
- M. Sabbaghan and H. Damerchiloo,
A note on periodic points and transitive maps,
Math. Sci. Q. J. 5 (2011), 259-266.
MathSciNet
- Y. Wang and G. Wei,
Characterizing mixing, weak mixing and transitivity of induced hyperspace dynamical systems,
Topology Appl. 155 (2007), 56-68.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
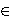 M, Fn(f)
M, Fn(f)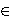 M and SFn(f)
M and SFn(f)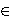 M.
M.
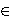 M, Fn(f)
M, Fn(f)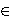 M and SFn(f)
M and SFn(f)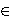 M.
M.