Glasnik Matematicki, Vol. 49, No. 2 (2014), 313-331.
ON SOME FUNCTIONAL EQUATIONS RELATED TO DERIVATIONS AND BICIRCULAR PROJECTIONS IN RINGS
Maja Fošner, Benjamin Marcen, Nejc Širovnik and Joso Vukman
Faculty of Logistics, University of Maribor, Mariborska cesta 7, 3000 Celje, Slovenia
e-mail: maja.fosner@fl.uni-mb.si
Faculty of Logistics, University of Maribor, Mariborska cesta 7, 3000 Celje, Slovenia
e-mail: benjamin.marcen@fl.uni-mb.si
Faculty of Natural Sciences and Mathematics, University of Maribor, Koroška cesta 160, 2000 Maribor, Slovenia
e-mail: nejc.sirovnik@uni-mb.si
Faculty of Mathematics, Natural Sciences and Information Technologies ,
University of Primorska, Glagoljaška 8, 6000 Koper
and
Institute of Mathematics, Physics and Mechanics, Jadranska 19, 1000 Ljubljana, Slovenia
e-mail: joso.vukman@uni-mb.si, joso.vukman@gmail.com
Abstract.
In this paper we prove the following result. Let n≥ 1
be some fixed integer and let R be a prime ring with 2n < char(R) ≠ 2. Suppose
there exist additive mappings S,T:R → R satisfying the relations
S(x2n)=S(x)x2n-1+xT(x)x2n-2+x2S(x)x2n-3+ ⋯ +x2n-1T(x),
T(x2n)=T(x)x2n-1+xS(x)x2n-2+ x2T(x)x2n-3+ ⋯ +x2n-1S(x)
for all x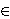 R. In this case S and T are of the form 2S(x)=D(x)+ζ (x),
2T(x)=D(x)-ζ (x) for all x
R. In this case S and T are of the form 2S(x)=D(x)+ζ (x),
2T(x)=D(x)-ζ (x) for all x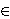 R, where D:R → R is a
derivation and ζ is an additive mapping, which maps R into its
extended centroid. Besides, ζ (x2n)=0 for all x
R, where D:R → R is a
derivation and ζ is an additive mapping, which maps R into its
extended centroid. Besides, ζ (x2n)=0 for all x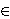 R. Functional equations
related to bicircular projections are also investigated.
R. Functional equations
related to bicircular projections are also investigated.
2010 Mathematics Subject Classification.
16R60, 16W10, 39B05.
Key words and phrases. Derivation, functional identity, bicircular projection.
Full text (PDF) (free access)
DOI: 10.3336/gm.49.2.06
References:
- K. I. Beidar, W. S. Martindale 3rd and A. V. Mikhalev, Rings with generalized identities, Marcel Dekker, Inc., New York, (1996).
MathSciNet
- K. I. Beidaar and Y.-Fong, On additive isomorphisms of prime rings preserving polynomials, J. Algebra 217 (1999), 650-667.
MathSciNet
CrossRef
- K. I. Beidar, M. Brešar, M. A. Chebotar and W. S. Martindale 3rd, On Herstein's Lie map Conjectures II, J. Algebra 238 (2001), 239-264.
MathSciNet
CrossRef
- K. I. Beidar, A. V. Mikhalev and M. A. Chebotar, Functional
identities in rings and their applications, Russian Math. Surveys 59 (2004), 403-428.
MathSciNet
CrossRef
- F. Botelho and J. Jamison, Generalized bicircular projections on minimal ideals of operators, Proc. Amer. Math. Soc. 136 (2008), 1397-1402.
MathSciNet
CrossRef
- F. Botelho and J. Jamison, Generalized bi-circular projections on spaces of analytic functions, Acta Sci. Math. (Szeged) 75 (2009), 527-546.
MathSciNet
- M. Brešar, M. A. Chebotar and W. S. Martindale 3rd, Functional identities, Birkhäuser Verlag, Basel-Boston-Berlin (2007).
MathSciNet
- J. Cusack, Jordan derivations on rings, Proc. Amer. Math. Soc. 53 (1975), 321-324.
MathSciNet
CrossRef
- A. Fošner and J. Vukman, Some functional equations on standard operator algebras, Acta Math. Hungar. 118 (2008), 299-306.
MathSciNet
CrossRef
- A. Fošner and D. Ilišević, Generalized bicircular projections via rank preserving maps on the spaces of symmetric and antisymmetric operators, Oper. Matrices 5 (2011), 239-260.
MathSciNet
CrossRef
- M. Fošner and D. Ilišević, On a class of projections on *-rings, Comm. Algebra 33 (2005), 3293-3310.
MathSciNet
CrossRef
- M. Fošner, D. Ilišević and C.-K. Li, G-invariant norms and bicircular projections, Linear Algebra Appl. 420 (2007), 596-608.
MathSciNet
CrossRef
- M. Fošner and J. Vukman, On some equations in prime rings, Monatsh. Math. 152 (2007), 135-150.
MathSciNet
CrossRef
- M. Fošner and J. Vukman, On some functional equations in rings, Commun. Algebra 39 (2011), 2647-2658.
MathSciNet
CrossRef
- I. N. Herstein, Jordan derivations of prime rings, Proc. Amer. Math. Soc. 8 (1957), 1104-1110.
MathSciNet
CrossRef
- D. Ilišević, Generalized bicircular projections via the operator equation α X2+AY2+β XAY+A=0, Linear Algebra Appl. 429 (2008), 2025-2029.
MathSciNet
CrossRef
- D. Ilišević, Generalized bicircular projections on JB* -triples, Linear Algebra Appl. 432 (2010), 1267-1276.
MathSciNet
CrossRef
- J. Jamison, Generalized bicircular projections on spaces of operator an JB* -triples, Rocky Mountain. J. Math. 41 (2011), 1241-1245.
MathSciNet
CrossRef
- I. Kosi-Ulbl and J. Vukman, A note on derivations in semiprime rings, Int. J. Math. & Math. Sci. 20 (2005), 3347-3350.
MathSciNet
CrossRef
- I. Kosi-Ulbl and J. Vukman, On some functional equations on standard operator algebras, Glas. Mat. Ser. III 44(64) (2009), 447-455.
MathSciNet
CrossRef
- L. H. Rowen, Some results on the center of a ring with polynomial identity, Bull. Amer. Math. Soc. 79 (1973), 219-223.
MathSciNet
CrossRef
- L. L. Stachó and B. Zalar, Bicircular projections on some matrix and operator spaces, Linear Algebra Appl. 384 (2004), 9-20.
MathSciNet
CrossRef
- L. L. Stachó and B. Zalar, Bicircular projections and characterization of Hilbert spaces, Proc. Amer. Math. Soc. 132 (2004), 3019-3025.
MathSciNet
CrossRef
- J. Vukman, On functional equations related to bicircular projections, Glas. Mat. Ser. III 41(61) (2006), 51-55.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
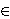 R. In this case S and T are of the form 2S(x)=D(x)+ζ (x),
2T(x)=D(x)-ζ (x) for all x
R. In this case S and T are of the form 2S(x)=D(x)+ζ (x),
2T(x)=D(x)-ζ (x) for all x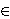 R, where D:R → R is a
derivation and ζ is an additive mapping, which maps R into its
extended centroid. Besides, ζ (x2n)=0 for all x
R, where D:R → R is a
derivation and ζ is an additive mapping, which maps R into its
extended centroid. Besides, ζ (x2n)=0 for all x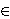 R. Functional equations
related to bicircular projections are also investigated.
R. Functional equations
related to bicircular projections are also investigated.