Glasnik Matematicki, Vol. 48, No. 2 (2013), 391-402.
QUASILINEAR ELLIPTIC EQUATIONS WITH POSITIVE EXPONENT ON THE GRADIENT
Jadranka Kraljević and Darko Žubrinić
Faculty of Economics,
University of Zagreb,
Kennedyev trg 6, 10000 Zagreb,
Croatia
e-mail: jkraljevic@efzg.hr
Department of Applied Mathematics,
Faculty of Electrical Engineering and Computing,
University of Zagreb,
Unska 3, 10000 Zagreb,
Croatia
e-mail: darko.zubrinic@fer.hr
Abstract. We study the existence and nonexistence of positive, spherically symmetric solutions
of a quasilinear elliptic equation (1.1) involving p-Laplace operator, with an arbitrary positive
growth rate e0 on the gradient on the right-hand side. We show
that e0=p-1 is the critical exponent: for e0< p-1 there exists a
strong solution for any choice of the coefficients, which is a known result, while for
e0>p-1 we have existence-nonexistence splitting of the
coefficients 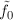 and
and 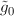 . The elliptic problem is studied by relating it to the corresponding singular ODE of the first order. We give sufficient conditions for a strong radial solution to be the weak solution. We also examined when ω-solutions of (1.1), defined in Definition 2.3, are weak solutions. We found conditions under which strong solutions are weak solutions in the critical case of e0=p-1.
. The elliptic problem is studied by relating it to the corresponding singular ODE of the first order. We give sufficient conditions for a strong radial solution to be the weak solution. We also examined when ω-solutions of (1.1), defined in Definition 2.3, are weak solutions. We found conditions under which strong solutions are weak solutions in the critical case of e0=p-1.
2010 Mathematics Subject Classification.
35J92, 35D35, 35D30, 35B33.
Key words and phrases. Quasilinear elliptic,
positive strong solution, ω-solution, critical exponent, existence, nonexistence, weak solution.
Full text (PDF) (free access)
DOI: 10.3336/gm.48.2.11
References:
-
B. Abdellaoui,
Multiplicity result for quasilinear elliptic problems with general growth in the gradient,
Adv. Nonlinear Stud. 8 (2008), 289-301.
MathSciNet
-
B. Abdellaoui, A. Dall'Aglio and I. Peral,
Some remarks on elliptic problems with critical growth in the gradient,
J. Differential Equations 222 (2006), 21-62.
MathSciNet
CrossRef
-
B. Abdellaoui, D. Giachetti, I. Peral and M. Walias,
Elliptic problems with nonlinear terms depending on the gradient and singular on the boundary,
Nonlinear Anal. 74 (2011), 1355-1371.
MathSciNet
CrossRef
- H. Brezis, Analyse fonctionnelle, Théorie et applications, Masson, Paris, 1983.
MathSciNet
-
Y. Chen and M. Wang,
Large solutions for quasilinear elliptic equation with nonlinear gradient term,
Nonlinear Anal. Real World Appl. 12 (2011), 455-463.
MathSciNet
CrossRef
-
D. Gilbarg and N. S. Trudinger,
Elliptic partial differential equations of second order, Springer-Verlag,
Berlin, 1983.
MathSciNet
-
K. Hansson, V. G. Maz'ya and I. E. Verbitsky,
Criteria of solvability for multi\-di\-men\-si\-o\-nal Riccati equations, Ark. Mat. 37 (1999), 87-120.
MathSciNet
CrossRef
-
L. Korkut, M. Pašić and D. Žubrinić,
A singular ODE related to quasilinear elliptic equations,
Electron. J. Differential Equations 2000, No. 12, 1-37.
MathSciNet
-
L. Korkut, M. Pašić and D. Žubrinić,
Some qualitative properties of solutions of quasilinear elliptic equations and applications,
J. Differential Equations 170 (2001), 247-280.
MathSciNet
CrossRef
-
Y. Tian and F. Li,
Comparison results for nonlinear degenerate Dirichlet and Neumann problems with general growth in the gradient, J. Math. Anal. Appl. 378 (2011), 749-763.
MathSciNet
CrossRef
-
D. Žubrinić,
Positive solutions of quasilinear elliptic systems with
the natural growth in the gradient, Rend. Istit. Mat. Univ. Trieste 32 (2000), 65-102.
MathSciNet
-
D. Žubrinić, Solvability of quasilinear
elliptic equations with strong dependence on the gradient, Abstr. Appl. Anal. 5 (2000), 159-173.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
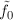 and
and 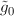 . The elliptic problem is studied by relating it to the corresponding singular ODE of the first order. We give sufficient conditions for a strong radial solution to be the weak solution. We also examined when ω-solutions of (1.1), defined in Definition 2.3, are weak solutions. We found conditions under which strong solutions are weak solutions in the critical case of e0=p-1.
. The elliptic problem is studied by relating it to the corresponding singular ODE of the first order. We give sufficient conditions for a strong radial solution to be the weak solution. We also examined when ω-solutions of (1.1), defined in Definition 2.3, are weak solutions. We found conditions under which strong solutions are weak solutions in the critical case of e0=p-1.