Glasnik Matematicki, Vol. 48, No. 2 (2013), 291-299.
ON THE DIOPHANTINE INEQUALITY |X2-cXY2+Y4| ≤ c+2
Bo He, István Pink, Ákos Pintér and Alain Togbé
Department of Mathematics, ABa Teacher's College, Wenchuan, Sichuan 623000,
P. R. China
e-mail: bhe@live.cn
Institute of Mathematics,
P. O. Box 12, H-4010 Debrecen,
Hungary
e-mail: pinki@science.unideb.hu
Institute of Mathematics, MTA-DE Research Group,
"Equations, Functions and Curves",
Hungarian Academy of Sciences and University of Debrecen,
P. O. Box 12, H-4010 Debrecen,
Hungary
e-mail: apinter@science.unideb.hu
Department of Mathematics,
Purdue University North Central,
1401 S. U.S. 421,
Westville, IN 46391,
USA
e-mail: atogbe@pnc.edu
Abstract. Generalizing some earlier results, we find all the coprime integer solutions of the Diophantine inequality
|X2-cXY2+Y4| ≤ c+2, (X,Y)=1,
except when c ≡ 2 (mod 4), in which case we bound the number of integer solutions. Our work is based on the results on the Diophantine equation
AX4-BY2=C,
where A, B are positive integers and C 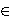 ±{1, 2, 4}.
±{1, 2, 4}.
2010 Mathematics Subject Classification.
11D25, 11J86.
Key words and phrases. Diophantine equations, quartic equations.
Full text (PDF) (free access)
DOI: 10.3336/gm.48.2.05
References:
- S. Akhtari, The Diophantine Equation aX4-bY2 = 1, J. Reine Angew. Math. 630 (2009), 33-57.
MathSciNet
CrossRef
- S. Akhtari, A. Togbé and P.G. Walsh, On the equation aX4 - bY2 = 2. Acta Arith. 131 (2008), 145-169.
MathSciNet
CrossRef
- S. Akhtari, A. Togbé, and P.G. Walsh, Addendum on the equation aX4 - bY2 = 2, Acta Arith. 137 (2009), 199-202.
MathSciNet
CrossRef
- M.A. Bennett, A. Togbé, and P.G. Walsh, A generalization of a theorem of Bumby on quartic Diophantine equations, Int. J. Number Theory, 2 (2006), 195-206.
MathSciNet
CrossRef
- W. Bosma, J. Cannon and C. Playoust, The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), 235-265.
MathSciNet
CrossRef
- J. H. E. Cohn, Twelve Diophantine equations, Arch. Math. 65 (1995), 130-133.
MathSciNet
CrossRef
- T. W. Cusick, The Diophantine equation x4-kx2y2+y4=1, Arch. Math. 59 (1992), 345-347.
MathSciNet
CrossRef
- A. Dujella, B. Ibrahimpašić and B. Jadrijević, Solving a family of quartic Thue inequalities using continued fractions, Rocky Mountain J. Math., 41 (2011), 1173-1182.
MathSciNet
CrossRef
- B. He, O. Kihel and A. Togbé, Solutions of a class of quartic Thue inequalities, Computers and Mathematics with Applications 61 (2011), 2914-2923.
MathSciNet
CrossRef
- C. Heuberger, Parametrized Thue equations: a survey, Proceedings of the RIMS symposium Analytic number theory and surrounding areas, Kyoto, Oct 18-22, 2004, RIMS Kôkyûroku 1511, August 2006, 82-91.
- D. H. Lehmer, An extended theory of Lucas' functions, Ann. of Math. (2) 31 (1930), 419-448.
MathSciNet
CrossRef
- W. Ljunggren, Ein Satz über die Diophantische Gleichung Ax2-By4=C (C=1,2,4) Tolfte Skand. Matemheikerkongressen, Lund (1953), 188-194.
MathSciNet
- W. Ljunggren. On the Diophantine equation Ax4-By2=C (C=1,4). Math. Scand. 21 (1967), 149-158. A remark concerning the paper "On the Diophantine equation Ax4-By2=C (C=1,4)", Math. Scand. 22 (1968), 282.
MathSciNet
- F. Luca and P. G. Walsh, Squares in Lehmer sequences with Diophantine applications, Acta Arit. 100 (2001), 47-62.
MathSciNet
CrossRef
- J. Luo and P. Yuan, Square-classes in Lehmer sequences having odd parameters and their applications, Acta Arith. 127 (2007), 49-62.
MathSciNet
CrossRef
- M. Mignotte, A. Pethö and R. Roth, Complete solutions of a family of quartic Thue and index form equations, Math. Comp. 65 (1996), 341-354.
MathSciNet
CrossRef
- A. Pethö, Complete solutions to families of quartic Thue equations, Math. Comp. 57 (1991), 777-798.
MathSciNet
CrossRef
- A. Togbé, P. M. Voutier and P. G. Walsh, Solving a family of Thue equations with an application to the equation x2-Dy4 = 1, Acta Arith. 120 (2005), 39-58.
MathSciNet
CrossRef
- P. M. Voutier, A further note on "On the equation aX4 - bY2 = 2", Acta Arith. 137 (2009), 203-206.
MathSciNet
CrossRef
- I. Wakabayashi, On a family of quartic Thue inequations, J. Number Theory 66 (1997), 70-84.
MathSciNet
CrossRef
- P. G. Walsh, A note on a theorem of Ljunggren and the Diophantine equations x2-kxy2+y4=1,4, Arch. Math. 73 (1999), 119-125.
MathSciNet
CrossRef
- P. Yuan and Y. Li, Squares in Lehmer sequences and the Diophantine equation Ax4-By2=2, Acta Arith. 139 (2009), 275-302.
MathSciNet
CrossRef
- P. Yuan and Z. Zhang, On the Diophantine Equation aX4-bY2=1, Acta Math. Sinica (Chin. Ser.) 53 (2010), 443-454 (in Chinese).
MathSciNet
Glasnik Matematicki Home Page
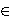 ±{1, 2, 4}.
±{1, 2, 4}.