Glasnik Matematicki, Vol. 48, No. 1 (2013), 81-90.
A NOTE ON REPRESENTATIONS OF SOME AFFINE VERTEX ALGEBRAS OF TYPE D
Ozren Perše
Department of Mathematics, University of Zagreb, 10 000 Zagreb, Croatia
e-mail: perse@math.hr
Abstract. In this note we construct a series of singular vectors in
universal affine vertex operator algebras associated to
D l(1) of levels n-l+1, for n 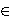 Z >0. For
n=1, we study the representation theory of the quotient vertex
operator algebra modulo the ideal generated by that singular vector.
In the case l =4, we show that the adjoint module is the unique
irreducible ordinary module for simple vertex operator algebra
LD4(-2,0). We also show that the maximal ideal in associated
universal affine vertex algebra is generated by three singular
vectors.
Z >0. For
n=1, we study the representation theory of the quotient vertex
operator algebra modulo the ideal generated by that singular vector.
In the case l =4, we show that the adjoint module is the unique
irreducible ordinary module for simple vertex operator algebra
LD4(-2,0). We also show that the maximal ideal in associated
universal affine vertex algebra is generated by three singular
vectors.
2010 Mathematics Subject Classification.
17B69, 17B67, 81R10.
Key words and phrases. Vertex operator algebra, affine Kac-Moody algebra, Zhu's
algebra.
Full text (PDF) (free access)
DOI: 10.3336/gm.48.1.07
References:
-
D. Adamović, Some rational vertex algebras, Glas. Mat.
Ser. III 29(49) (1994), 25-40.
MathSciNet
-
D. Adamović, A construction of some ideals in affine
vertex algebras, Int. J. Math. Math. Sci. 2003 (2003),
971-980.
MathSciNet
CrossRef
-
D. Adamović, A construction of admissible A1(1)-modules of level -4/3, J. Pure Appl. Algebra 196
(2005), 119-134.
MathSciNet
CrossRef
-
D. Adamović and A. Milas, Vertex operator algebras
associated to modular invariant representations for A1(1),
Math. Res. Lett. 2 (1995), 563-575.
MathSciNet
CrossRef
- D. Adamović and O. Perše, Some general results
on conformal embeddings of affine vertex operator algebras, Algebr. Represent. Theory 16 (2013), 51-64.
MathSciNet
CrossRef
- J. D. Axtell and K.-H. Lee, Vertex operator algebras associated to type G affine Lie algebras, J. Algebra 337 (2011), 195-223.
MathSciNet
CrossRef
-
R. E. Borcherds, Vertex algebras, Kac-Moody algebras, and
the Monster, Proc. Nat. Acad. Sci. U.S.A. 83 (1986),
3068-3071.
MathSciNet
CrossRef
-
N. Bourbaki, Iliments de mathimatique. (French) Fasc. XXXVIII: Groupes et
alg.bres de Lie. Chapitre VII: Sous-alg.bres de Cartan, iliments
riguliers. Chapitre VIII: Alg.bres de Lie semi-simples diployies.
Actualitis Scientifiques et Industrielles, No. 1364. Hermann, Paris, 1975.
-
C. Dong, H. Li and G. Mason, Vertex operator algebras
associated to admissible representations of
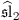 ,
Comm. Math. Phys. 184 (1997), 65-93.
,
Comm. Math. Phys. 184 (1997), 65-93.
MathSciNet
CrossRef
- A. J. Feingold and I. B. Frenkel, Classical affine
algebras, Adv. in Math. 56 (1985), 117-172.
MathSciNet
CrossRef
- E. Frenkel and D. Ben-Zvi, Vertex algebras and algebraic curves, American Mathematical Society, Providence, 2001.
MathSciNet
-
I. Frenkel, Y.-Z. Huang and J. Lepowsky, On axiomatic
approaches to vertex operator algebras and modules, Mem. Amer.
Math. Soc. 104, 1993.
MathSciNet
-
I. Frenkel, J. Lepowsky and A. Meurman, Vertex operator algebras
and the Monster, Academic Press,
Boston, 1988.
MathSciNet
-
I. Frenkel and Y.-C. Zhu, Vertex operator algebras
associated to representations of affine and Virasoro algebras, Duke
Math. J. 66 (1992), 123-168.
MathSciNet
CrossRef
-
V. G. Kac, Infinite dimensional Lie algebras, 3rd ed., Cambridge
Univ. Press, Cambridge, 1990.
MathSciNet
CrossRef
- V. G. Kac, Vertex algebras for beginners, AMS, Providence, 1998.
MathSciNet
- V. Kac and M. Wakimoto, Modular invariant representations of
infinite dimensional Lie algebras and superalgebras, Proc. Nat.
Acad. Sci. U.S.A. 85 (1988), 4956-4960.
MathSciNet
CrossRef
- J. Lepowsky and H. Li, Introduction to vertex operator algebras
and their representations, Birkhäuser,
Boston, 2004.
MathSciNet
CrossRef
-
H.-S. Li, Local systems of vertex operators, vertex
superalgebras and modules, J. Pure Appl. Algebra 109
(1996), 143-195.
MathSciNet
CrossRef
- A. Meurman and M. Primc, Annihilating fields of standard modules
of sl(2, C)~ and combinatorial identities, Mem. Amer.
Math. Soc. 137, AMS, Providence RI, 1999.
MathSciNet
-
O. Perše, Vertex operator algebras associated to type B
affine Lie algebras on admissible half-integer levels, J. Algebra
307 (2007), 215-248.
MathSciNet
CrossRef
- O. Perše, Vertex operator algebras associated to certain admissible modules for affine Lie algebras of type
A, Glas. Mat. Ser. III 43(63) (2008), 41-57.
MathSciNet
CrossRef
-
Y.-C. Zhu, Modular invariance of characters of vertex
operator algebras, J. Amer. Math. Soc. 9 (1996), 237-302.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
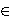 Z >0. For
n=1, we study the representation theory of the quotient vertex
operator algebra modulo the ideal generated by that singular vector.
In the case l =4, we show that the adjoint module is the unique
irreducible ordinary module for simple vertex operator algebra
LD4(-2,0). We also show that the maximal ideal in associated
universal affine vertex algebra is generated by three singular
vectors.
Z >0. For
n=1, we study the representation theory of the quotient vertex
operator algebra modulo the ideal generated by that singular vector.
In the case l =4, we show that the adjoint module is the unique
irreducible ordinary module for simple vertex operator algebra
LD4(-2,0). We also show that the maximal ideal in associated
universal affine vertex algebra is generated by three singular
vectors.
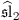 ,
Comm. Math. Phys. 184 (1997), 65-93.
,
Comm. Math. Phys. 184 (1997), 65-93.