Glasnik Matematicki, Vol. 48, No. 1 (2013), 31-48.
ON THE DIOPHANTINE EQUATION F(N)=U!+V!
Florian Luca
Fundación Marcos Moshinsky,
Universidad Nacional Autonoma de México,
Circuito Exterior, C.U., Apdo. Postal 70-543,
Mexico D.F. 04510,
Mexico
e-mail: fluca@matmor.unam.mx
Abstract. In this paper, we show under the abc conjecture that the Diophantine equation f(x)=u!+v! has only finitely many integer solutions (x,u,v)
whenever f(X)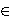 Q[X] is a polynomial of degree at least three.
Q[X] is a polynomial of degree at least three.
2010 Mathematics Subject Classification.
11D85.
Key words and phrases. Factorials, polynomials, applications of the abc conjecture.
Full text (PDF) (free access)
DOI: 10.3336/gm.48.1.03
References:
- C. Ballot and F. Luca, Prime factors of af(n)-1 with an irreducible polynomial f(x), New York J. Math. 12 (2006), 39-45.
MathSciNet
CrossRef
- D. Berend and J. Harmse, On polynomial factorial diophantine equations, Trans. Amer. Math. Soc. 358 (2005), 1741-1779.
MathSciNet
CrossRef
- P. Erdös and R. Obláth, Uber diophantishe Gleichungen der Form n! = xp ± yp und n! ± m! = xp, Acta Litt. Sci. Szeged 8 (1937), 241-255.
- M. Gawron, On the equation P(z)=n!+m!, preprint.
- A. Granville and O. Ramaré, Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients, Mathematika 43 (1996), 73-107.
MathSciNet
CrossRef
- H. Iwaniec and J. Pintz, Primes in short intervals, Monatsh. Math. 98 (1984), 115-143.
MathSciNet
CrossRef
- F. Luca, The Diophantine equation P (x) = n! and a result of M. Overholt, Glas. Mat. Ser. III 37 (2002), 269-273.
MathSciNet
Glasnik Matematicki Home Page
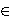 Q[X] is a polynomial of degree at least three.
Q[X] is a polynomial of degree at least three.
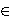 Q[X] is a polynomial of degree at least three.
Q[X] is a polynomial of degree at least three.