Glasnik Matematicki, Vol. 47, No. 1 (2012), 119-132.
ON CERTAIN FUNCTIONAL EQUATION
ARISING FROM (M,N)- JORDAN CENTRALIZERS IN PRIME RINGS
Nina Peršin and Joso Vukman
Prušnikova 48, 2000 Maribor, Slovenia
e-mail: nina_persin@t-2.net
Department of Mathematics and Computer Science,
Faculty of Natural Sciences and Mathematics,
University of Maribor,
Koroška cesta 160, 2000 Maribor,
Slovenia
e-mail: joso.vukman@uni-mb.si
Abstract. The purpose of this paper is to prove the following result. Let m≥
1,n≥ 1 be some fixed integers and let R be a prime ring with char(R)=0 or (m+n)2 < char (R).
Suppose there exists an additive mapping T:R → R satisfying the relation
2(m+n)2T(x3)=m(2m+n)T(x)x2+2mnxT(x)x+n(2n+m)x2T(x) for all x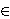 R. In this case T is a two-sided centralizer.
R. In this case T is a two-sided centralizer.
2010 Mathematics Subject Classification.
16W10, 46K15, 39B05.
Key words and phrases. Ring, prime ring, semiprime ring, Banach space, Hilbert
space, algebra of all bounded linear operators, standard operator algebra,
derivation, Jordan derivation, left (right) centralizer, two-sided
centralizer, left (right) Jordan centralizer, (m,n)-Jordan centralizer.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.1.09
References:
- K. I. Beidar, W. S. Martindale, III and A. V. Mikhalev, Rings
with generalized identities, Marcel Dekker, Inc., New York 1996.
MathSciNet
- K. I. Beidar and Y. Fong, On additive isomorphisms of prime
rings preserving polynomials, J. Algebra 217 (1999), 650-667.
MathSciNet
CrossRef
- M. Brešar and J. Vukman, Jordan derivations on prime
rings, Bull. Austral. Math. Soc. 37 (1988), 321-322.
MathSciNet
CrossRef
- M. Brešar, Jordan derivations on semiprime rings,
Proc. Amer. Math. Soc. 104 (1988), 1003-1006.
MathSciNet
CrossRef
- M. Brešar, Jordan mappings of semiprime rings, J.
Algebra 127 (1989), 218-228.
MathSciNet
CrossRef
- M. Brešar, Functional identities: a survey,
Contemp. Math. 259 (2000), 93-109.
MathSciNet
CrossRef
- M. Brešar, M. Chebotar and W. S. Martindale, III, Functional identities, Birkhäuser Verlag, Basel, 2007.
MathSciNet
- J. Cusack, Jordan derivations on rings, Proc. Amer.
Math. Soc. 53 (1975), 321-324.
MathSciNet
CrossRef
- A. Fošner and J. Vukman, On certain functional
equations related to Jordan triple (θ, φ)-derivations on
semiprime rings, Monatsh. Math. 162 (2011), 157-165.
MathSciNet
CrossRef
- I. N. Herstein, Jordan derivations of prime rings,
Proc. Amer. Math. Soc. 8 (1957), 1104-1110.
MathSciNet
CrossRef
- I. Kosi-Ulbl and J. Vukman, On centralizers of standard
operator algebras and semisimple H*-algebras, Acta Math. Hungar.
110 (2006), 217-223.
MathSciNet
CrossRef
- C.-K. Liu and W.-K. Shiue, Generalized Jordan triple (θ, φ)-derivations on semiprime rings, Taiwanese J. Math.
11 (2007), 1397-1406.
MathSciNet
- E. C. Posner, Derivations in prime rings, Proc. Amer.
Math. Soc. 8 (1957), 1093-1100.
MathSciNet
CrossRef
- L. Rowen, Some results on the center of a ring with
polynomial identity, Bull. Amer. Math. Soc. 79 (1973), 219-223.
MathSciNet
CrossRef
- J. Vukman, An identity related to centralizers in
semiprime rings, Comment. Math. Univ. Carolin. 40 (1999), 447-456.
MathSciNet
- J. Vukman, I. Kosi-Ulbl and D. Eremita, On certain
equations in rings, Bull. Austral. Math. Soc. 71 (2005), 53-60.
MathSciNet
CrossRef
- J. Vukman and I. Kosi-Ulbl, Centralisers on rings and
algebras, Bull. Austral. Math. Soc. 71 (2005), 225-234.
MathSciNet
CrossRef
- J. Vukman and I. Kosi-Ulbl, On centralizers of semisimple
H* -algebras, Taiwanese J. Math. 11 (2007), 1063-1074.
MathSciNet
- J. Vukman, On (m,n)-Jordan centralizers in rings and
algebras, Glas. Mat. Ser. III 45(65) (2010), 43-53.
MathSciNet
CrossRef
- B. Zalar, On centralizers of semiprime rings, Comment.
Math. Univ. Carolin. 32 (1991), 609-614.
MathSciNet
Glasnik Matematicki Home Page
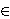 R. In this case T is a two-sided centralizer.
R. In this case T is a two-sided centralizer.
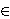 R. In this case T is a two-sided centralizer.
R. In this case T is a two-sided centralizer.