Glasnik Matematicki, Vol. 47, No. 1 (2012), 105-118.
ON (ANTI-)MULTIPLICATIVE GENERALIZED DERIVATIONS
Daniel Eremita and Dijana Ilišević
Department of Mathematics and Computer Science,
FNM, University of Maribor,
2000 Maribor,
Slovenia
e-mail: daniel.eremita@uni-mb.si
Department of Mathematics,
University of Zagreb,
Bijenička 30, P.O.Box
335, 10002 Zagreb,
Croatia
e-mail: ilisevic@math.hr
Abstract. Let R be a semiprime ring and let F, f : R → R be (not necessarily additive)
maps satisfying F(xy)=F(x)y+xf(y) for all x,y 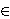 R.
Suppose that there are integers m and n such that F(uv)=mF(u)F(v)+nF(v)F(u)
for all u, v in some nonzero ideal I of R.
Under some mild assumptions on R, we prove that there exists
c
R.
Suppose that there are integers m and n such that F(uv)=mF(u)F(v)+nF(v)F(u)
for all u, v in some nonzero ideal I of R.
Under some mild assumptions on R, we prove that there exists
c 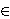 C(I⊥⊥) such that c=(m+n)c2,
nc[I⊥⊥, I⊥⊥]=0 and F(x)=cx for all x
C(I⊥⊥) such that c=(m+n)c2,
nc[I⊥⊥, I⊥⊥]=0 and F(x)=cx for all x 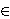 I⊥⊥.
The main result is then applied to the case when F is multiplicative or anti-multiplicative on I.
I⊥⊥.
The main result is then applied to the case when F is multiplicative or anti-multiplicative on I.
2010 Mathematics Subject Classification.
16U99, 16N60, 39B52, 47B47.
Key words and phrases. Additivity, ring, semiprime ring, prime ring, derivation, generalized
derivation, homomorphism, anti-homomorphism.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.1.08
References:
- A. Asma, N. Rehman and A. Shakir, On Lie ideals with derivations as
homomorphisms and anti-homomorphisms, Acta Math. Hungar. 101
(2003), 79-82.
MathSciNet
CrossRef
- K. I. Beidar, W. S. Martindale, III and A. V. Mikhalev, Rings
with generalized identities, Marcel Dekker, Inc., 1996.
MathSciNet
- H. E. Bell and L.-C. Kappe, Rings in which derivations satisfy
certain algebraic conditions, Acta Math. Hungar. 53 (1989), 339-346.
MathSciNet
CrossRef
- M. Brešar, On the distance of the composition of two
derivations to the generalized derivations, Glasgow Math. J.
33 (1991), 89-93.
MathSciNet
CrossRef
- D. Eremita and D. Ilišević, On additivity of centralisers,
Bull. Austral. Math. Soc. 74 (2006), 177-184.
MathSciNet
CrossRef
- V. de Filippis, Generalized derivations as Jordan homomorphisms on
Lie ideals and right ideals, Acta Math. Sin. (Engl. Ser.) 25
(2009), 1965-1974.
MathSciNet
CrossRef
- O. Gëlbasi and K. Kaya, On Lie ideals with generalized derivations,
Siberian Math. J. 47 (2006), 862-866.
MathSciNet
CrossRef
- I. Gusić, A note on generalized derivations of prime rings,
Glas. Mat. Ser. III 40(60) (2005), 47-49.
MathSciNet
CrossRef
- I. N. Herstein, Topics in ring theory, The University of Chicago Press,
Chicago, 1969.
MathSciNet
- T.-K. Lee, Generalized derivations of left faithful rings,
Comm. Algebra 27 (1999), 4057-4073.
MathSciNet
CrossRef
- N. Rehman, On generalized derivations as homomorphisms and
anti-homomorphisms, Glas. Mat. Ser. III 39(59) (2004), 27-30.
MathSciNet
CrossRef
- Y. Wang and H. You, Derivations as homomorphisms or
anti-homomorphisms on Lie ideals, Acta Math. Sin. (Engl. Ser.)
23 (2007), 1149-1152.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
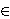 R.
Suppose that there are integers m and n such that F(uv)=mF(u)F(v)+nF(v)F(u)
for all u, v in some nonzero ideal I of R.
Under some mild assumptions on R, we prove that there exists
c
R.
Suppose that there are integers m and n such that F(uv)=mF(u)F(v)+nF(v)F(u)
for all u, v in some nonzero ideal I of R.
Under some mild assumptions on R, we prove that there exists
c 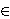 C(I⊥⊥) such that c=(m+n)c2,
nc[I⊥⊥, I⊥⊥]=0 and F(x)=cx for all x
C(I⊥⊥) such that c=(m+n)c2,
nc[I⊥⊥, I⊥⊥]=0 and F(x)=cx for all x 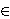 I⊥⊥.
The main result is then applied to the case when F is multiplicative or anti-multiplicative on I.
I⊥⊥.
The main result is then applied to the case when F is multiplicative or anti-multiplicative on I.