Glasnik Matematicki, Vol. 47, No. 1 (2012), 95-104.
ON FUNCTIONAL EQUATIONS RELATED TO DERIVATIONS IN SEMIPRIME RINGS AND STANDARD OPERATOR ALGEBRAS
Nejc Širovnik
Department of Mathematics and Computer Science,
Faculty of Natural Sciences and Mathematics,
University of Maribor,
Koroška 160, 2000 Maribor,
Slovenia
e-mail: nejc.sirovnik@uni-mb.si
Abstract. In this paper functional equations related to derivations
on semiprime rings and standard operator algebras are investigated. We prove, for example,
the following result, which is related to a classical result of Chernoff. Let
X be a real or complex Banach space, let L(X) be the algebra of all
bounded linear operators of X into itself and let A(X) ⊂ L(X) be a standard operator algebra. Suppose there exist linear mappings D,G:A(X) → L(X) satisfying the relations D(A3)=D(A2)A+A2G(A),G(A3)=G(A2)A+A2D(A) for all A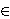 A(X). In this case there exists B
A(X). In this case there exists B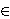 L(X) such that D(A)=G(A)=[A,B] holds for all A
L(X) such that D(A)=G(A)=[A,B] holds for all A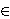 A(X).
A(X).
2010 Mathematics Subject Classification.
16N60, 46B99, 39B42.
Key words and phrases. Prime ring, semiprime ring, Banach space,
standard operator algebra, derivation, Jordan derivation, Jordan triple
derivation.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.1.07
References:
-
K. I. Beidar, M. Brešar, M. A. Chebotar and W. S. Martindale III, On Herstein's Lie map Conjectures. II, J. Algebra 238 (2001), 239-264.
MathSciNet
CrossRef
-
K. I. Beidar, W. S. Martindale III and A. V. Mikhalev, Rings with generalized identities, Marcel Dekker, Inc., New York, 1996.
MathSciNet
-
M. Brešar, Jordan derivations on semiprime rings, Proc. Amer. Math. Soc. 104 (1988), 1003-1006.
MathSciNet
CrossRef
-
M. Brešar, Jordan mappings of semiprime rings, J. Algebra 127 (1989), 218-228.
MathSciNet
CrossRef
-
M. Brešar and J. Vukman, Jordan derivations on prime rings, Bull. Austral. Math. Soc. Vol. 37 (1988), 321-322.
MathSciNet
CrossRef
-
M. Brešar and J. Vukman, Jordan (θ,φ)-derivations, Glas. Mat. Ser. III 26(46) (1991), 13-17.
MathSciNet
-
P. R. Chernoff, Representations, automorphisms and derivations of some Operator Algebras, J. Functional Analysis 12 (1973), 275-289.
MathSciNet
CrossRef
-
J. Cusack, Jordan derivations on rings, Proc. Amer. Math. Soc. 53 (1975), 321-324.
MathSciNet
CrossRef
-
I. N. Herstein, Jordan derivations on prime rings, Proc. Amer. Math. Soc. 8 (1957), 1104-1119.
MathSciNet
CrossRef
-
I. Kosi-Ulbl and J. Vukman, A note on derivations in semiprime rings, Int. J. Math. Math. Sci. 20 (2005), 3347-3350.
MathSciNet
CrossRef
-
I. Kosi-Ulbl and J. Vukman, On derivations in rings with involution, Int. Math. J. 6 (2005), 81-91.
MathSciNet
-
I. Kosi-Ulbl and J. Vukman, An identity related to derivations of standard operator algebras and semisimple H*-algebras, Cubo 12 (2010), 95-102.
MathSciNet
CrossRef
-
P. Šemrl, Ring derivations on standard operator algebras, J. Functional Analysis 112 (1993), 318-324.
MathSciNet
CrossRef
-
J. Vukman, On automorphisms and derivations of operator algebras, Glas. Mat. Ser. III 19(39) (1984), 135-138.
MathSciNet
-
J. Vukman, Identities with derivations and automorphisms on semiprime rings, Int. J. Math. Math. Sci. (2005), 1031-1038.
MathSciNet
CrossRef
-
J. Vukman, I. Kosi-Ulbl and D. Eremita, On certain equations in rings, Bull. Austral. Math. Soc. Vol. 71 (2005), 53-60.
MathSciNet
CrossRef
-
J. Vukman, On derivations of algebras with involution, Acta Math. Hungar. 112 (2006), 181-186.
MathSciNet
CrossRef
-
J. Vukman, On derivations of standard operator algebras and semisimple H*-algebras, Studia Sci. Math. Hungar. 44 (2007), 57-63.
MathSciNet
CrossRef
-
J. Vukman, Identities related to derivations and centralizers on standard operator algebras, Taiwanese J. Math. 11 (2007), 255-265.
MathSciNet
-
J. Vukman, Some remarks on derivations in semiprime rings and standard operator algebras, Glas. Mat. Ser. III 46(66) (2011), 43-48.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
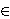 A(X). In this case there exists B
A(X). In this case there exists B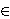 L(X) such that D(A)=G(A)=[A,B] holds for all A
L(X) such that D(A)=G(A)=[A,B] holds for all A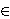 A(X).
A(X).
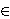 A(X). In this case there exists B
A(X). In this case there exists B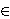 L(X) such that D(A)=G(A)=[A,B] holds for all A
L(X) such that D(A)=G(A)=[A,B] holds for all A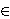 A(X).
A(X).