Glasnik Matematicki, Vol. 46, No. 2 (2011), 333-338.
A REMARK ON THE DIOPHANTINE EQUATION f(x)=g(y)
Ivica Gusić
Faculty of Chemical Engineering and Technology, University of Zagreb, Marulićev trg 19, 10000 Zagreb, Croatia
e-mail: igusic@fkit.hr
Abstract. Let K be an algebraic number field, and let
h(x)=x3+ax be a polynomial over K. We prove that there exists
infinitely many b 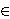 K such that the equation dy2=x3+ax+b
has no solutions over K for infinitely many d
K such that the equation dy2=x3+ax+b
has no solutions over K for infinitely many d 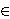 K*/K* 2. The proof is based on recent results of
B. Mazur and K. Rubin on the 2-Selmer rank in families of
quadratic twists of elliptic curves over number fields.
On the other side, it is known that if the parity conjecture is
valid, then there exist a number field K and a cubic polynomial f
irreducible over K, such that the equation dy2=f(x) has
infinitely many solutions for each d
K*/K* 2. The proof is based on recent results of
B. Mazur and K. Rubin on the 2-Selmer rank in families of
quadratic twists of elliptic curves over number fields.
On the other side, it is known that if the parity conjecture is
valid, then there exist a number field K and a cubic polynomial f
irreducible over K, such that the equation dy2=f(x) has
infinitely many solutions for each d 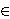 K*.
K*.
2000 Mathematics Subject Classification.
11G05, 14G05.
Key words and phrases. Elliptic curve, quadratic twist, 2-Selmer rank, number field.
Full text (PDF) (free access)
DOI: 10.3336/gm.46.2.05
References:
-
T. Dokchitser and V. Dokchitser, Elliptic curves with all quadratic
twists of positive rank, Acta Arith. 137 (2009), 193-197.
MathSciNet
CrossRef
-
T. Dokchitser and V. Dokchitser, Root numbers and parity of ranks
of elliptic curves,
J. Reine Angew. Math. 2011, 658, 39-64.
-
A. Granville, Rational and integral points on quadratic twists of a given hyperelliptic curve, Int. Math. Res. Not. IMRN 2007, Art. ID 027, 24 pp. (2007).
MathSciNet
-
I. Gusić, A characterization of linear polynomials, J. Number Theory 115 (2005), 343-347.
MathSciNet
CrossRef
-
I. Gusić, Some applications of the abc-conjecture to the diophantine equation qym = f(x), Glas. Mat. Ser III., to appear.
-
B. Mazur and K. Rubin, Ranks of twists of elliptic curves and
Hilbert's tenth problem, Invent. Math. 181 (2010), 541-575.
MathSciNet
CrossRef
-
J. Nakagawa and K. Horie, Elliptic curves with no rational
points, Proc. Amer. Math. Soc. 104 (1988), 20-24.
MathSciNet
CrossRef
-
K. Ono and C. Skinner, Non-vanishing of quadratic twists of modular L-functions, Invent. Math., 134 (1998), 651-660.
MathSciNet
CrossRef
-
A. Schinzel, Polynomials with special regard to reducibility, Cambridge University Press, Cambridge, 2000.
MathSciNet
- J. H. Silverman, The Arithmetic of Elliptic Curves,
Graduate Texts in Mathematics, 106, Springer, Berlin, 1986.
MathSciNet
Glasnik Matematicki Home Page
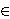 K such that the equation dy2=x3+ax+b
has no solutions over K for infinitely many d
K such that the equation dy2=x3+ax+b
has no solutions over K for infinitely many d 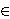 K*/K* 2. The proof is based on recent results of
B. Mazur and K. Rubin on the 2-Selmer rank in families of
quadratic twists of elliptic curves over number fields.
On the other side, it is known that if the parity conjecture is
valid, then there exist a number field K and a cubic polynomial f
irreducible over K, such that the equation dy2=f(x) has
infinitely many solutions for each d
K*/K* 2. The proof is based on recent results of
B. Mazur and K. Rubin on the 2-Selmer rank in families of
quadratic twists of elliptic curves over number fields.
On the other side, it is known that if the parity conjecture is
valid, then there exist a number field K and a cubic polynomial f
irreducible over K, such that the equation dy2=f(x) has
infinitely many solutions for each d 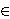 K*.
K*.