Glasnik Matematicki, Vol. 45, No.1 (2010), 219-290.
SOME CELLULAR SUBDIVISIONS OF SIMPLICIAL COMPLEXES
Sibe Mardešić
Department of Mathematics, University of Zagreb, Bijenička cesta 30, 10002 Zagreb, P.O. Box 335, Croatia
e-mail: smardes@math.hr
Abstract. In a previous paper the author has associated with
every inverse system of compact CW-complexes X with limit X and every
simplicial complex K with geometric realization |K| a resolution of
X × |K|, which
consists of spaces having the homotopy type of polyhedra. In a subsequent paper it
is shown that this construction is functorial. The proof depends essentially on
particular cellular subdivisions of K. The purpose of this paper is to
describe in detail these subdivisions and establish their relevant
properties. In particular, one defines two subdivisions
L(K) and N(K) of K.
Each cell from L(K), respectively from N(K), is contained
in a simplex σ 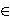 K and it is
the direct sum a
K and it is
the direct sum a 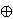 b,
respectively c
b,
respectively c 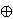 d,
of certain simplices contained in σ.
One defines new subdivisions L'(K) and N'(K) of K
by taking for their cells the direct sums
L(a)
d,
of certain simplices contained in σ.
One defines new subdivisions L'(K) and N'(K) of K
by taking for their cells the direct sums
L(a) 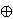 b,
respectively c
b,
respectively c 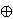 N(d).
The main result asserts that there is an
isomorphism of cellular complexes
N(d).
The main result asserts that there is an
isomorphism of cellular complexes
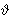 : L'(K) → N'(K),
which induces a
selfhomeomorphism
θ : |K| → |K|.
: L'(K) → N'(K),
which induces a
selfhomeomorphism
θ : |K| → |K|.
2000 Mathematics Subject Classification.
55U10, 52B11, 54C56.
Key words and phrases. Convex polytope, simplicial complex,
cellular complex, subdivision of a complex, isomorphism of cellular complexes, resolution of a space, shape.
Full text (PDF) (free access)
DOI: 10.3336/gm.45.1.14
References:
- P. Alexandroff and H. Hopf, Topologie, Springer, Berlin, 1935.
- A. Brondsted,
An introduction to convex polytopes, Graduate Texts in Mathematics, Springer, Berlin, 1983.
MathSciNet
- J. Dugundji,
Topology, Allyn and Bacon, Boston, 1966.
MathSciNet
- B. Grünbaum,
Convex polytopes,
Interscience Publishers John Wiley & Sons, Inc., New York, 1967.
MathSciNet
- S. Mardesic,
Strong shape and homology, Springer Monographs in Mathematics,
Springer-Verlag, Berlin, 2000.
MathSciNet
- S. Mardesic,
A resolution for the product
of a compactum with a polyhedron, Topology Appl. 133 (2003), 37-63.
MathSciNet
CrossRef
- S. Mardesic,
Functoriality of the standard resolution of
the Cartesian product of a compactum and a polyhedron, Topology Appl. 155 (2007), 1-32.
MathSciNet
CrossRef
- S. Mardesic, J. Segal,
Shape theory, North-Holland, Amsterdam, 1982.
MathSciNet
- M. Moszynska,
Selected topics in convex geometry, Birkhäuser, Basel, 2006.
MathSciNet
Glasnik Matematicki Home Page
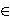 K
K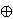 b,
b,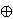 d,
d,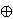 b,
b,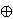 N(d).
N(d).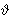 : L'(K) → N'(K),
: L'(K) → N'(K),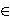 K
K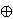 b,
b,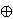 d,
d,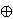 b,
b,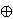 N(d).
N(d).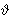 : L'(K) → N'(K),
: L'(K) → N'(K),