Glasnik Matematicki, Vol. 44, No.1 (2009), 1-6.
A REMARK ON THE DIOPHANTINE EQUATION
(x3-1)/(x-1)=(yn-1)/(y-1)
Bo He
Sichuan Provincial Key Laboratory of Computer Software, Sichuan Normal University,
Chengdu, 610068, P. R. China
e-mail: hebo-one@hotmail.com
e-mail: bhe@live.cn
Abstract. In this remark, we use some properties of simple continued fractions
of quadratic irrational numbers to prove that the equation
(x3 - 1)/(x - 1) = (yn - 1)/(y - 1),
x, y, n 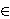 N, x > 1, y > 1,
n > 3, n odd,
N, x > 1, y > 1,
n > 3, n odd,
has only the solutions (x,y,n) = (5,2,5) and (90,2,13).
2000 Mathematics Subject Classification.
11A55, 11D09, 11D61.
Key words and phrases. Goormaghtigh equation, continued fraction, congruence.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.1.01
References:
- A. Baker,
Bounds for the solutions of the
hyperelliptic equation, Proc. Cambridge Philos. Soc. 65 (1969), 439-444.
MathSciNet
CrossRef
- Y. Bugeaud, T. N. Shorey,
On the number of solutions of the
generalized Ramanujan-Nagell equation, J. Reine Angew. Math.
539 (2001), 55-74.
MathSciNet
CrossRef
- Y. Bugeaud, T. N. Shorey,
On the diophantine equation
(xm-1)/(x-1)=(yn-1)/(y-1),
Pacific J. Math.
207 (2002), 61-75.
MathSciNet
- J. Coates,
An effective p-adic analogue of a theorem of Thue II:
The greatest prime factor of a binary form, Acta Arith. 16 (1969/1970), 399-412.
MathSciNet
- H. Davenport, D. J. Lewis, and A. Schinzel,
Equations of the form f(x) = g(y),
Quart. J. Math. Oxford Ser. (2) 12 (1961), 304-312.
MathSciNet
CrossRef
- A. Dujella,
Continued fractions and RSA with small secret
exponent, Tatra Mt. Math. Publ. 29 (2004), 101-112.
MathSciNet
- A. Dujella and B. Ibrahimpasic,
On Worley's theorem in
Diophantine approximations, Ann. Math. Inform. 35 (2008), 61-73.
MathSciNet
- A. Dujella and B. Jadrijevic,
A family of quartic Thue
inequalities, Acta Arith. 111 (2004), 61-76.
MathSciNet
CrossRef
- P. Fatou,
Sur l'approximation des incommensurables et les series trigonometriques,
C. R. Acad. Sci. (Paris) 139 (1904), 1019-1021.
- R. Goormaghtigh,
L'Intermédiaire des Mathématiciens,
24 (1917), 88.
- I. Niven, H. S. Zuckerman and H. L. Montgomery,
An Introduction to the Theory of Numbers, John Wiley & Sons, Inc., New York, 1991.
MathSciNet
- M. Le,
On the Diophantine equation
(x3-1)/(x-1)=(yn-1)/(y-1),
Trans. Amer. Math. Soc. 351 (1999), 1063-1074.
MathSciNet
CrossRef
- M. Le,
Exceptional solutions of the exponential Diophantine equation
(x3-1)/(x-1)=(yn-1)/(y-1),
J. Reine Angew. Math. 543 (2002), 187-192.
MathSciNet
CrossRef
- M. Le,
On Goormaghtigh's equation
(x3-1)/(x-1)=(yn-1)/(y-1),
Acta Math. Sinica (Chin. Ser.) 45 (2002), 505-508.
MathSciNet
- T. Nagell,
The diophantine equation x2 + 7 = 2n,
Ark. Mat. 4 (1961), 185-187.
MathSciNet
CrossRef
- Yu. V. Nesterenko and T. N. Shorey,
On an equation of Goormaghtigh, Acta Arith. 83 (1998), 381-389.
MathSciNet
- R. Ratat,
L'Intermédiaire des Mathématiciens, 23 (1916), 150.
- A. Schinzel,
On two theorems of Gelfond and some of their
applications, Acta Arith. 13 (1967/1968), 177-236.
MathSciNet
- A. Schinzel,
An improvement of Runge's theorem on diophantine
equations, Comment. Pontificia Acad. Sci. 2 (1969), 1-9.
MathSciNet
- T. N. Shorey,
On the equation axm - byn = k,
Nederl. Akad. Wetensch. Indag. Math. 48 (1986), 353-358.
MathSciNet
- T. N. Shorey,
Integers with identical digits, Acta Arith. 53 (1989), 187-205.
MathSciNet
- C. L. Siegel,
Approximation algebraischer Zahlen, Math. Z.
10 (1921), 173-213.
MathSciNet
CrossRef
- C. L. Siegel,
The integer solutions of the equation
y2 = axn + bxn-1
+ ... + k, (Under the pseudonym X), J. London
Math. Soc. 1 (1926), 66-68.
- A. Thue,
Über Annäherungswerte algebraischer Zahlen,
J. Reine Angew. Math. 135 (1909), 284-305.
- R. T. Worley,
Estimating |α - p/q|, J. Austral.
Math. Soc. Ser. A 31 (1981), 202-206.
MathSciNet
CrossRef
- P. Z. Yuan,
On the diophantine equation
(x3-1)/(x-1)=(yn-1)/(y-1),
J. Number Theory
112 (2005), 20-25.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
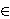 N, x > 1, y > 1,
n > 3, n odd,
N, x > 1, y > 1,
n > 3, n odd, 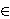 N, x > 1, y > 1,
n > 3, n odd,
N, x > 1, y > 1,
n > 3, n odd,