Glasnik Matematicki, Vol. 42, No.2 (2007), 291-299.
ON LINEAR SUBSPACES OF Mn AND THEIR
SINGULAR SETS RELATED TO THE CHARACTERISTIC MAP
Marcin Skrzynski
Institute of Mathematics, Cracow University of Technology, ul. Warszawska 24,
31-155 Krakow, Poland
e-mail: pfskrzyn@cyf-kr.edu.pl
Abstract. We study linear subspaces
L
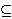 Mn
(over an algebraically closed field F
of characteristic zero) and their singular sets
S(L)
defined by
S(L) =
{A
Mn
(over an algebraically closed field F
of characteristic zero) and their singular sets
S(L)
defined by
S(L) =
{A 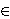 Mn :
χ(A + L) is not dense
in Fn},
where χ :
Mn
→ Fn
is the characteristic map.
We give a complete characterization of the subspaces
L
Mn :
χ(A + L) is not dense
in Fn},
where χ :
Mn
→ Fn
is the characteristic map.
We give a complete characterization of the subspaces
L 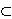 M2
such that
M2
such that
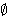 ≠
S(L)
≠ M2.
We also provide a complete characterization of the singular
sets S(L)
in the case of n = 2.
Finally, we give a characterization of the n-dimensional
subspaces L
≠
S(L)
≠ M2.
We also provide a complete characterization of the singular
sets S(L)
in the case of n = 2.
Finally, we give a characterization of the n-dimensional
subspaces L
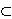 Mn
such that
S(L)
=
Mn
such that
S(L)
= 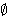 by means of their
intersections with conjugacy classes.
by means of their
intersections with conjugacy classes.
2000 Mathematics Subject Classification.
15A18, 14A10, 14L35.
Key words and phrases. Characteristic polynomial of a matrix,
characteristic map, dominant map,
linear space of matrices, triangularizable set of matrices, conjugacy class of a matrix.
Full text (PDF) (free access)
DOI: 10.3336/gm.42.2.04
References:
- S. Friedland, Inverse eigenvalue problems,
Linear Algebra Appl. 17 (1977), 15-51.
MathSciNet
CrossRef
- F. R. Gantmacher, Théorie des matrices, Dunod, Paris, 1966.
MathSciNet
- W. Helton, J. Rosenthal and X. Wang,
Matrix extensions and eigenvalue completions, the generic case,
Trans. Amer. Math. Soc. 349 (1997), 3401-3408.
MathSciNet
CrossRef
- H.-P. Kraft, Geometrische Methoden in der Invariantentheorie,
Friedr. Vieweg & Sohn, Braunschweig - Wiesbaden, 1984.
MathSciNet
- S. Lang, Algebra, Addison Wesley, Reading, MA, 1993.
MathSciNet
- I. R. Shafarevich, Basic Algebraic Geometry, Springer-Verlag,
Berlin - Heidelberg - New York, 1977.
MathSciNet
- M. Skrzynski,
On a singular set for the restriction of the characteristic map to a linear subspace
of Mn, Math. Slovaca 54 (2004), 229-236.
MathSciNet
Glasnik Matematicki Home Page
 Mn
Mn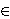 Mn :
χ(A + L) is not dense
in Fn},
Mn :
χ(A + L) is not dense
in Fn},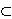 M2
M2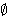 ≠
S(L)
≠ M2.
≠
S(L)
≠ M2.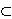 Mn
Mn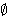
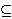 Mn
Mn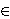 Mn :
χ(A + L) is not dense
in Fn},
Mn :
χ(A + L) is not dense
in Fn},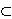 M2
M2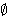 ≠
S(L)
≠ M2.
≠
S(L)
≠ M2.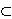 Mn
Mn