Glasnik Matematicki, Vol. 42, No.1 (2007), 117-130.
SHAPE PROPERTIES OF THE BOUNDARY OF ATTRACTORS
J. J. Sánchez-Gabites and José M. R. Sanjurjo
Departamento de Geometria y Topologia, Facultad de Matemáticas,
Universidad Complutense de Madrid, 28040 Madrid, Spain
e-mail: jajsanch@mat.ucm.es
e-mail: jose_sanjurjo@mat.ucm.es
Abstract. Let M be a locally compact metric space endowed with a
continuous flow
φ : M × R → M.
Assume that K is a stable attractor for φ and
P 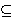 A(K)
is a compact positively invariant
neighbourhood of K contained in its basin of attraction. Then it
is known that the inclusion
K
A(K)
is a compact positively invariant
neighbourhood of K contained in its basin of attraction. Then it
is known that the inclusion
K 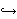 P
is a shape
equivalence and the question we address here is whether there
exists some relation between the shapes of ∂K and
∂P. The general answer is negative, as shown by example,
but under certain hypotheses on K the shape domination
Sh(∂K) ≥ Sh(∂P)
or even the equality
Sh(∂K) = Sh(∂P) hold. However we
also put under study interesting situations where those hypotheses
are not satisfied, albeit other techniques such as Lefschetz's
duality render results relevant to our question.
P
is a shape
equivalence and the question we address here is whether there
exists some relation between the shapes of ∂K and
∂P. The general answer is negative, as shown by example,
but under certain hypotheses on K the shape domination
Sh(∂K) ≥ Sh(∂P)
or even the equality
Sh(∂K) = Sh(∂P) hold. However we
also put under study interesting situations where those hypotheses
are not satisfied, albeit other techniques such as Lefschetz's
duality render results relevant to our question.
2000 Mathematics Subject Classification.
54H20, 55P55, 58F12.
Key words and phrases. Dynamical systems, attractors, boundary of attractors, shape.
Full text (PDF) (free access)
DOI: 10.3336/gm.42.1.10
References:
- N. P. Bhatia and G. P. Szegö,
Stability Theory of Dynamical Systems, Die Grundlehren der mathematischen Wissenschaften, Band 161,
Springer--Verlag, New York-Berlin, 1970.
MathSciNet
- S. A. Bogatyi and V. I. Gutsu,
On the structure of
attracting compacta, Differentsialnye Uravneniya 25 (1989), 907-909.
MathSciNet
- K. Borsuk,
Theory of Retracts, PWN-Polish Scientific
Publishers, Warszawa, 1967.
MathSciNet
- K. Borsuk,
Concerning homotopy properties of compacta,
Fund. Math. 62 (1968), 223-254.
MathSciNet
- K. Borsuk,
Theory of Shape, PWN-Polish Scientific Publishers,
Warszawa, 1975.
MathSciNet
- M. Brown,
A proof of the generalized Schönflies
theorem, Bull. Amer. Math. Soc. 66 (1960), 74-76.
MathSciNet
- W. C. Chewning and R. S. Owen,
Local sections of flows on manifolds,
Proc. Amer. Math. Soc. 49 (1975), 71-77.
MathSciNet
CrossRef
- R. C. Churchill,
Isolated invariant sets in compact metric
spaces, J. Differential Equations 12 (1972), 330-352.
MathSciNet
CrossRef
- C. Conley,
Isolated Invariant Sets and the Morse Index, CBMS
Regional Conference Series in Mathematics 38, American
Mathematical Society, Providence, 1978.
MathSciNet
- C. Conley and R. Easton,
Isolated invariant sets and isolating blocks,
Trans. Amer. Math. Soc. 158 (1971), 35-61.
MathSciNet
CrossRef
- J. Dydak and J. Segal,
Shape Theory. An Introduction, Lecture
Notes in Mathematics 688, Springer, Berlin, 1978.
MathSciNet
- A. Giraldo, M. A. Morón, F. R. Ruiz del Portal and
J. M. R. Sanjurjo,
Shape of global attractors in topological spaces, Nonlinear Anal.
60 (2005), 837-847.
MathSciNet
CrossRef
- A. Giraldo and J. M. R. Sanjurjo,
On the global structure of invariant
regions of flows with asymptotically stable attractors,
Math. Z. 232 (1999), 739-746.
MathSciNet
CrossRef
- B. Günther and J. Segal,
Every attractor of a flow on a manifold has the shape of a finite polyhedron,
Proc. Amer. Math. Soc. 119 (1993), 321-329.
MathSciNet
CrossRef
- H. M. Hastings,
A higher-dimensional Poincaré-Bendixson theorem,
Glas. Mat. Ser. III 14(34) (1979), 263-268.
MathSciNet
- S. Hu,
Theory of Retracts, Wayne State University Press,
Detroit, 1965.
MathSciNet
- S. Mardesic, Strong Shape and Homology, Springer-Verlag,
Berlin-Heidelberg-New York 2000.
MathSciNet
- S. Mardesic and J. Segal,
Equivalence of the Borsuk and the ANR-system approach to shapes,
Fund. Math. 72 (1971), 61-68.
MathSciNet
- S. Mardesic and J. Segal,
Shapes of compacta and ANR-systems,
Fund. Math. 72 (1971), 41-59.
MathSciNet
- S. Mardesic and J. Segal, Shape Theory, North-Holland
Publishing Co., Amsterdam-New York-Oxford 1982.
MathSciNet
- F. Raymond,
Separation and union theorems for generalized
manifolds with boundary, Michigan Math. J. 7 (1960), 7-21.
MathSciNet
CrossRef
- J. C. Robinson and O. M. Tearne,
Boundaries of attractors as omega limit sets,
Stoch. Dyn. 5 (2005), 97-109.
MathSciNet
CrossRef
- D. Salamon,
Connected simple systems and the Conley index
of isolated invariant sets, Trans. Amer. Math. Soc. 291 (1985), 1-41.
MathSciNet
CrossRef
- J. J. Sánchez-Gabites and J. M. R. Sanjurjo,
On the topology of the boundary of a basin of attraction,
Proc. Amer. Math. Soc., to appear.
- J. M. R. Sanjurjo,
Multihomotopy, Cech spaces of loops
and shape groups, Proc. London Math. Soc. (3) 69 (1994), 330-344.
MathSciNet
CrossRef
- J. M. R. Sanjurjo,
On the structure of uniform attractors, J. Math. Anal. Appl. 192
(1995), 519--528.
MathSciNet
CrossRef
- E. H. Spanier,
Algebraic Topology, McGraw-Hill Book Co., New
York-Toronto-London, 1966.
MathSciNet
- J. E. West,
Mapping Hilbert cube manifolds to ANR's: a
solution of a conjecture of Borsuk,
Ann. Math. (2) 106 (1977), 1-18.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
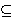 A(K)
A(K)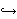 P
P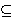 A(K)
A(K)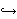 P
P