Glasnik Matematicki, Vol. 42, No.1 (2007), 19-41.
FINITE-SHEETED COVERING MAPS OVER KLEIN BOTTLE WEAK SOLENOIDAL SPACES
Vlasta Matijević
Department of Mathematics, University of Split, N. Tesle 12, 21000 Split,
Croatia
e-mail: vlasta@pmfst.hr
Abstract. Klein bottle weak solenoidal space
Σ(p,q,r) is a continuum obtained as the inverse limit of
an inverse sequence, where each term is Klein bottle and each
bonding map is finite-sheeted covering map over Klein bottle. In
the present paper we determine and present all s-sheeted
covering maps (with connected total space) over
Σ(p,q,r),
s 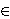 N,
both pointed and unpointed case.
N,
both pointed and unpointed case.
2000 Mathematics Subject Classification.
14H30, 22C05, 57M10.
Key words and phrases. Inverse system, covering map, Klein bottle, weak solenoidal
space, Klein bottle weak solenoidal space, 2-dimensional torus,
2-dimensional compact Abelian group, fundamental progroup,
subprogroup of index s, conjugacy classes of subprogroups of
index s.
Full text (PDF) (free access)
DOI: 10.3336/gm.42.1.02
References:
- K. Eda and V. Matijevic,
Finite sheeted covering maps over 2-dimensional connected, compact abelian group,
Topology Appl. 153 (2006), 1033-1045.
MathSciNet
CrossRef
- K. Eda and V. Matijevic,
Finite-index supergroups and subgroups of torsionfree Abelian groups of rank two,
submitted.
- J. Keesling and S. Mardesic,
A shape fibration with fibers of different shape,
Pacific J. Math. 84 (1979) 319-331.
MathSciNet
- S. Mardesic and V. Matijevic,
Classifying overlay structures of topological spaces,
Topology Appl. 113 (2001), 167-209.
MathSciNet
CrossRef
- V. Matijevic,
Classifying finite-sheeted covering mappings of paracompact spaces,
Rev. Mat. Complut. 16 (2003), 311-327.
MathSciNet
- M. C. McCord,
Inverse limit sequences with covering maps,
Trans. Amer. Math. Soc. 114 (1965), 197-209.
MathSciNet
CrossRef
- C. Tezer,
Shape classification of Klein-bottle-like continua,
Quart. J. Math. Oxford Ser (2) 40 (1989), 225-243.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
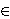 N,
N,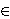 N,
N,