Glasnik Matematicki, Vol. 41, No.1 (2006), 165-176.
ON LINKING OF CANTOR SETS
Matjaž Željko
Faculty of Mathematics and Physics,
University of Ljubljana, Jadranska 19, 1000 Ljubljana, Slovenia
e-mail: matjaz.zeljko@fmf.uni-lj.si
Abstract. We introduce a property L for a subset of a manifold which
enables us to pass the geometric linking property from the
manifold to this subset. We prove that cubes with handles M and
N are linked if and only if subsets X
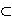 Int M and
Y
Int M and
Y 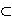 Int N
having property L are linked. We
present a criterion which shows that many known Cantor sets
explicitly given by defining sequences have this property. As an
application of the property L we extend the theorem on
rigid Cantor sets thus allowing slightly more complicated terms in
their defining sequences.
Int N
having property L are linked. We
present a criterion which shows that many known Cantor sets
explicitly given by defining sequences have this property. As an
application of the property L we extend the theorem on
rigid Cantor sets thus allowing slightly more complicated terms in
their defining sequences.
2000 Mathematics Subject Classification.
57M30.
Key words and phrases. Geometric linking, Cantor set, defining sequence,
rigid Cantor set.
Full text (PDF) (free access)
DOI: 10.3336/gm.41.1.14
References:
- S. Armentrout,
Decompositions of E3 with a compact
0-dimensional set of nondegenerate elements,
Trans. Amer. Math. Soc. 123 (1966), 165-177.
MathSciNet
CrossRef
- H. G. Böthe,
Eine fixierte Kurve in E3,
General Topology and Its Relations to Modern Analysis and Algebra. II
(Proc. Second Prague Topological Symposium 1966), Academia,
Prague, 1967, 68-73.
MathSciNet
- R. J. Daverman,
On the scarcity of tame disks in certain
wild cells, Fund. Math. 79 (1973), 63-77.
MathSciNet
- R. J. Daverman and R. D. Edwards,
Wild Cantor sets as
approximations to codimension two manifolds,
Topologly Appl. 26 (1987), 207-218.
MathSciNet
CrossRef
- D. Garity, D. Repovs and D. Zeljko,
Rigid Cantor sets in R3 with simply connected complement,
Preprint Series IMFM Ljubljana Vol. 42 (2004) No. 943.
- J. M. Martin,
A rigid sphere,
Fund. Math. 59 (1966), 117-121.
MathSciNet
- R. B. Sher,
Concerning wild Cantor sets in E3,
Proc. Amer. Math. Soc. 19 (1968), 1195-1200.
MathSciNet
CrossRef
- A. C. Shilepsky,
A rigid Cantor set in E3,
Bull. Acad. Polon. Sci. 22 (1974), 223-224.
MathSciNet
- D. G. Wright,
Rigid sets in En,
Pacific J. Math. 121 (1986), 245-256.
MathSciNet
- D. G. Wright,
Rigid sets in manifolds,
Geometric and Algebraic Topology,
Banach Center Publ. 18, PWN, Warsaw, 1986, 161-164.
MathSciNet
Glasnik Matematicki Home Page
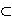 Int M
Int M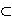 Int N
Int N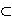 Int M
Int M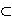 Int N
Int N