Glasnik Matematicki, Vol. 40, No.2 (2005), 189-199.
IDENTITIES WITH DERIVATIONS ON RINGS AND BANACH ALGEBRAS
Joso Vukman
Department of Mathematics, University of Maribor,
PEF, Koroška 160, 2000 Maribor, Slovenia
e-mail: joso.vukman@uni-mb.si
Abstract. In this paper we prove the following result. Let
m ≥ 1,
n ≥ 1
be integers and let R be a
2mn(m+n-1)!-torsion free semiprime ring. Suppose there exist
derivations D, G : R
→ R such that
D(xm)xn +
xnG(xm) = 0
holds for all x 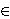 R. In
this case both derivations D and G map R into its center and
D = -G. We apply this purely algebraic result to obtain a range
inclusion result of continuous derivations on Banach algebras.
R. In
this case both derivations D and G map R into its center and
D = -G. We apply this purely algebraic result to obtain a range
inclusion result of continuous derivations on Banach algebras.
2000 Mathematics Subject Classification.
16N60, 46K15.
Key words and phrases. Prime ring, semiprime ring, Banach algebra,
derivation, commuting mapping, centralizing mapping,
skew-commuting mapping, skew-centralizing mapping.
Full text (PDF) (free access)
DOI: 10.3336/gm.40.2.01
References:
- K. I. Beidar, W.S. Martindale III and A.V. Mikhalev,
Ringswith generalized identities, Marcel Dekker, Inc. New York 1996.
- H. E. Bell and W.S. Martindale III,
Centralizing mappings of semiprime rings,
Canad. Math. Bull. 30 (1987), 92-101.
- M. Brešar and J. Vukman,
Orthogonal derivations and an extension of a theorem of Posner,
Radovi Mat. 5 (1989), 237-246.
- M. Brešar,
Centralizing mappings on von Neumann algebras,
Proc. Amer. Math. Soc. 111 (1991), 501-510.
CrossRef
- M. Brešar and J. Vukman,
Derivations of noncommutative Banach algebras,
Arch. Math. 59 (1992), 363-370.
CrossRef
- M. Brešar,
On a generalization of the notion of
centralizing mappings, Proc. Amer. Math. Soc. 114 (1992), 641-649.
CrossRef
- M. Brešar,
On skew-commuting mappings of rings,
Bull. Austral. Math. Soc. 47 (1993), 291-296.
- M. Brešar,
Centralizing mappings and derivations in
prime rings, J. Algebra 156 (1993), 385-394.
CrossRef
- M. Brešar,
Commuting traces of biadditive mappings,
commutativity-preserving mappings and Lie mappings,
Trans. Amer. Math. Soc. 335 (1993), 525-394.
CrossRef
- M. Brešar,
Derivations of noncommutative Banach algebras II,
Arch. Math. 63 (1994), 56-59.
CrossRef
- M. Brešar,
On generalized biderivations and related maps,
J. Algebra 172 (1995), 764-786.
CrossRef
- M. Brešar and A. R. Villena,
The range of a derivations on a Jordan Banach algebras,
Studia Math. 146 (2001), 177-200.
- C.-L. Chuang,
On decomposition of derivations of prime rings,
Proc. Amer. Math. Soc. 108 (1990), 647-652.
CrossRef
- Q. Deng and H. E. Bell,
On derivations and commutativity in semiprime rings,
Commun. in Algebra 23 (1995), 3705-3713.
- N. Divinsky,
On commuting automorphisms on rings,
Trans. Roy. Soc. Canada, Sect. III 49 (1995), 19-22.
- I. N. Herstein, Rings with involution, Chicago Lectures
in Math., Univ. of Chicago Press, Chicago, London, 1976.
- B. E. Johnson and A. M. Sinclair,
Continuity of derivations and a problem of Kaplansky,
Amer. J. Math. 90 (1968), 1068-1073.
CrossRef
- B. Kim,
On derivations on Semiprime rings and
Noncommutative Banach Algebras,
Acta Math. Sinica, English Series 16 (2000), 21-28.
- T.-K. Lee,
Semiprime rings with differential identities,
Bull. Inst. Math. Acad. Sinica 20 (1992), 27-38.
- T.-K. Lee,
Semiprime rings with hypercentral derivations,
Canad. Mat. Bull. 38 (1995), 445-449.
- J. Luh,
A note on commuting automorphisms of rings,
Amer. Math. Monthly 77 (1970), 61-62.
CrossRef
- M. Mathieu and G.J. Murphy,
Derivations mapping into the radical,
Arch. Math. 57 (1991), 469-474.
CrossRef
- M. Mathieu, Where to find the image of a derivation,
Functional analysis and operator theory, Banach center
publications, Vol. 30, Institute of Mathematics, Polish academy of
sciences, Warszawa 1994.
- J. H. Mayne,
Centralizing automorphisms of prime rings,
Canad. Math. Bull. 19 (1976), 113-115.
- E. C. Posner,
Derivations in prime rings,
Proc. Amer. Math. Soc. 8 (1957), 1093-1100.
CrossRef
- V. Runde,
Range inclusion results for derivations on
noncommutative Banach algebras, Studia Math. 105 (1993), 159-172.
- A. M. Sinclair,
Jordan homomorphisms and derivations on
semisimple Banach algebras,
Proc. Amer. Math. Soc. 24 (1970), 209-214.
CrossRef
- I. M. Singer and J. Wermer,
Derivations on commutative
normed algebras,
Math. Ann. 129 (1955), 435-460.
CrossRef
- A. B. Thaheem,
On a pair of derivations on semiprime rings, preprint.
- A. B. Thaheem,
On certain pair of normal operators,
New Zealand J. Math. 30 (2001), 87-92.
- M. P. Thomas,
The image of a derivation is contained in
the radical,
Annals of Math. 128 (1988), 435-460.
CrossRef
- J. Vukman,
Commuting and centralizing mappings in prime rings,
Proc. Amer. Math. Soc. 109 (1990), 47-52.
CrossRef
- J. Vukman,
A result concerning derivations in
noncommutative Banach algebras,
Glasnik Mat. 26(46) (1991), 83-88.
- J. Vukman,
On derivations in prime rings and Banach
algebras,
Proc. Amer. Math. Soc. 116 (1992), 877-884.
CrossRef
- J. Vukman,
Derivations on semiprime rings,
Bull. Austral. Math. Soc. 53 (1995), 353-359.
- J. Vukman,
Centralizers on semiprime rings,
Comment. Math. Univ. Carolinae 42 (2001), 237-245.
- B. Yood,
Continuous homomorphisms and derivations on
Banach algebras, Contemp. Math. 32 (1984), 279-284.
Glasnik Matematicki Home Page
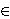 R.
R.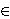 R.
R.