Glasnik Matematicki, Vol. 40, No.1 (2005), 29-45.
THE θ-TRANSFER TECHNIQUE: ON NOETHERIAN
INVOLUTION RINGS AND SYMMETRY OF PRIMITIVITY
Boris Širola
Department of Mathematics, University of Zagreb,
Bijenička 30, 10000 Zagreb, Croatia
e-mail: sirola@math.hr
Abstract. Let
θ :
R
→
S
be a ring
anti-isomorphism. We study
θ-homomorphisms
between left
R-modules E
and right
S-modules M,
that is, homomorphisms of the additive groups
θ :
E →
M
satisfying
θ(r.x) =
θ(x).θ(r) for
r 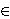 R
and x
R
and x 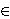 E.
We also study the class of Noetherian involution rings and the
problem of symmetry of primitivity. In particular, suppose that
for every semiprimitive Noetherian involution ring which has
exactly two minimal prime ideals both of these satisfy (SP). Then
every prime ideal of an arbitrary Noetherian ring satisfies (SP);
we say that a prime ideal
P of some ring satisfies
(SP), the symmetry of primitivity, if it holds that
P
is left primitive if and only if it is right primitive. Besides,
as an interesting fact, we note that any factor ring of the
enveloping algebra of the Lie algebra
E.
We also study the class of Noetherian involution rings and the
problem of symmetry of primitivity. In particular, suppose that
for every semiprimitive Noetherian involution ring which has
exactly two minimal prime ideals both of these satisfy (SP). Then
every prime ideal of an arbitrary Noetherian ring satisfies (SP);
we say that a prime ideal
P of some ring satisfies
(SP), the symmetry of primitivity, if it holds that
P
is left primitive if and only if it is right primitive. Besides,
as an interesting fact, we note that any factor ring of the
enveloping algebra of the Lie algebra
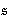
 (2) over a
field of characteristic zero is an involution algebra, and so it
satisfies the Krull symmetry.
(2) over a
field of characteristic zero is an involution algebra, and so it
satisfies the Krull symmetry.
2000 Mathematics Subject Classification.
16W10, 16D60.
Key words and phrases. Antihomomorphism, antiautomorphic
ring, involution ring, θ-homomorphism, prime ideal, primitive
ideal, symmetry of primitivity.
Full text (PDF) (free access)
DOI: 10.3336/gm.40.1.04
References:
- N. Bourbaki,
Algèbre, Chapitres I,II,III, Hermann, Paris, 1970.
- S. Catoiu,
Ideals of the enveloping algebra
U(sl2),
J. Algebra 202 (1998), 142-177.
CrossRef
- J. Dixmier,
Idéaux primitifs dans les algèbres enveloppantes,
J. Algebra 48 (1977), 96-112.
CrossRef
- M. Duflo,
Sur la classification des idéaux primitifs dans l'algèbre enveloppante
d'un algèbre de Lie semi-simple,
Ann. of Math. (2) 105 (1977), 107-120.
- P. Gabriel,
Des catégories abéliennes,
Bull. Soc. Math. France 90 (1962), 323-448.
- K. R. Goodearl and R. B. Warfield, Jr.,
An Introduction to Noncommutative Noetherian Rings,
London Math. Soc. Stud. Texts, vol. 16, Cambridge Univ. Press, Cambridge,
1989.
- R. Gordon and J. C. Robson,
Krull dimension, Memoirs Amer. Math. Soc. 133, 1973.
- A. G. Heinicke,
On the Krull-symmetry of enveloping algebras,
J. London Math. Soc. (2) 24 (1981), 109-112.
CrossRef
- G. Krause,
On fully left bounded left noetherian rings,
J. Algebra 23 (1972), 88-99.
CrossRef
- T. H. Lenagan,
Artinian ideals in noetherian rings,
Proc. Amer. Math. Soc. 51 (1975), 499-500.
CrossRef
- T. Levasseur,
Krull dimension of the enveloping algebra
of a semisimple Lie algebra,
Proc. Amer. Math. Soc. 130 (2002), 3519-3523.
CrossRef
- J. C. McConnell and J. C. Robson,
Noncommutative Noetherian rings, J. Wiley, New York, 1987.
- C. Moeglin,
Idéaux primitifs des algèbres enveloppantes,
J. Math. Pures. Appl. 59 (1980), 265-336.
- S. Montgomery,
A structure theorem and a positive-definiteness condition in
rings with involution,
J. Algebra 43 (1976), 181-192.
- R. S. Pierce,
Associative Algebras, Graduate Texts in Mathematics 88,
Springer-Verlag, 1982.
- R. Rentschler and P. Gabriel,
Sur la dimension des anneaux et ensembles ordonnés,
C. R. Acad. Sci. Paris, Sér. A, 265 (1967), 712-715.
- P. F. Smith,
On the dimension of group rings,
Proc. London Math. Soc. 25 (1972), 288-302.
CrossRef
- B. Širola,
Going up for enveloping algebras of Lie algebras,
J. Algebra 243 (2001), 539-550.
CrossRef
- B. Širola,
On noncommutative Noetherian schemes,
J. Algebra 282 (2004), 667-698.
CrossRef
- B. Širola,
A generalized global Cartan decomposition;
a basic example, preprint.
Glasnik Matematicki Home Page
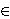 R
R 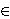 E.
E.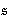
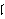 (2)
(2)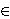 R
R 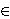 E.
E.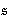
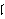 (2)
(2)