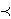 (1 + Az) / (1 + Bz),
(1 + Az) / (1 + Bz),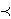 "
denotes the usual subordination. In this paper we
investigate the linear combination of the analytic representations
of starlikeness and convexity and give sharp sufficient
conditions over the differential operator
"
denotes the usual subordination. In this paper we
investigate the linear combination of the analytic representations
of starlikeness and convexity and give sharp sufficient
conditions over the differential operator
Abstract. Let
A be the class of
analytic functions in the unit disk
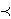 (1 + Az) / (1 + Bz),
(1 + Az) / (1 + Bz),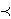 "
denotes the usual subordination. In this paper we
investigate the linear combination of the analytic representations
of starlikeness and convexity and give sharp sufficient
conditions over the differential operator
"
denotes the usual subordination. In this paper we
investigate the linear combination of the analytic representations
of starlikeness and convexity and give sharp sufficient
conditions over the differential operator
a zf'(z) / f(z) + b (1 + zf''(z) / f'(z))
that imply2000 Mathematics Subject Classification. 30C45.
Key words and phrases. Starlike function, starlike function of order α, criteria, differential subordination, Jack lemma.