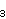Glasnik Matematicki, Vol. 39, No.2 (2004), 221-233.
MINIMAL NONMODULAR FINITE p-GROUPS
Zvonimir Janko
Mathematical Institute, University of Heidelberg,
69120 Heidelberg, Germany
e-mail: janko@mathi.uni-heidelberg.de
Abstract. We describe first the structure of finite
minimal nonmodular 2-groups G. We show that in case
|G| > 25, each proper subgroup
of G is Q8-free
and G/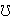
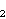 (G)
is minimal nonabelian of order 24 or 25.
If |G/
(G)
is minimal nonabelian of order 24 or 25.
If |G/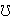
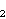 (G)| =
24, then the structure
of G is determined up to isomorphism (Propositions 2.4 and 2.5).
If |G/
(G)| =
24, then the structure
of G is determined up to isomorphism (Propositions 2.4 and 2.5).
If |G/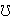
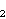 (G)| =
25, then
Ω1(G)
(G)| =
25, then
Ω1(G)
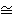 E8 and
G/Ω1(G)
is metacyclic (Theorem 2.8).
E8 and
G/Ω1(G)
is metacyclic (Theorem 2.8).
Then we classify finite minimal nonmodular
p-groups G with p > 2 and
|G| > p4 (Theorems 3.5 and 3.7).
We show that
G/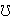
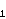 (G)
is nonabelian of order p3 and
exponent p and
(G)
is nonabelian of order p3 and
exponent p and
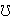
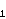 (G)
is metacyclic. Also,
G/Ω1(G)
(G)
is metacyclic. Also,
G/Ω1(G)
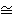 Ep
Ep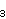 and
G/Ω1(G)
is metacyclic.
and
G/Ω1(G)
is metacyclic.
2000 Mathematics Subject Classification.
20D15.
Key words and phrases. p-group, modular group,
nonmodular group, quaternion group, minimal nonabelian group.
Full text (PDF) (free access)
Glasnik Matematicki Home Page
 (G)
(G)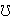
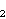 (G)| =
24,
(G)| =
24,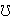
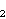 (G)| =
25,
(G)| =
25,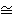 E8
E8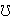
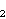 (G)
(G)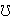
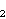 (G)| =
24,
(G)| =
24,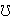
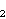 (G)| =
25,
(G)| =
25,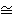 E8
E8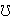
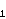 (G)
(G)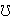
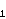 (G)
(G)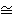 Ep
Ep