Glasnik Matematicki, Vol. 34, No.1 (1999), 5-10.
LIFTING A CIRCULAR MEMBRANE BY UNITARY FORCES
Lucio R. Berrone
CONICET, Departamento de Matematica, Facultad de Ciencias Exactas,
Ing. y Agrim., Universidad Nacional Rosario, Av. Pellegrini 250,
2000 Rosario, Argentina
Abstract. Let
Ω be a convex membrane. We lift certain parts
Γ of its boundary by means of unitary forces while the
remaining parts are maintained at level 0. Call
u[Γ]
the position that the such lifted membrane assumes. When the parts
Γ are varying on
∂Ω
so that their total lenght C is preserved, it has been
conjectured that the functional
Γ
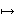 ||u(Γ)||p attain its maximum value for a
certain conected arc of lenght C. In this paper we present a
proof of this conjecture for the case in which
Ω is a circle and p = 1.
||u(Γ)||p attain its maximum value for a
certain conected arc of lenght C. In this paper we present a
proof of this conjecture for the case in which
Ω is a circle and p = 1.
1991 Mathematics Subject Classification.
31A05, 31A15.
Full text (PDF) (free access)
Glasnik Matematicki Home Page
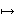 ||u(Γ)||p
||u(Γ)||p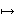 ||u(Γ)||p
||u(Γ)||p