bt
≡ 1 (mod n), ili
postoji r, 0 ≤
r < s, takav da je
b2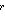 t
≡ -1 (mod n),
(***)
t
≡ -1 (mod n),
(***)
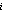 ≡ a
(mod n).
Tada ako je n prost, onda mora biti a = -1 jer
je b(n-1)/2
≡ a
(mod n).
Tada ako je n prost, onda mora biti a = -1 jer
je b(n-1)/2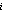

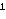 ≡ 1
(mod n), a jedina rješenja
kongruencije
≡ 1
(mod n), a jedina rješenja
kongruencije
|
Definicija: Neka je n neparan složen broj, te neka je
n - 1 = 2s . t,
gdje je t neparan broj. Neka je b
cijeli broj takav da je (b,n) = 1. Ako vrijedi
bt
≡ 1 (mod n), ili
postoji r, 0 ≤
r < s, takav da je
b2 |
Očito je svaki spsp(b) ujedno i psp(b). Može se pokazati da je svaki spsp(b) ujedno i epsp(b). Obrat ne vrijedi. Npr. n =561 je epsp(2) jer je 2280 ≡ (2/561) ≡ 1 (mod 561), ali n nije spsp(2) jer je 2280 ≡ 1 (mod 561), a 2140 ≡ 67 (mod 561).
| Teorem 4.3: Ako je n ≡ 3 (mod 4), onda je n spsp(b) ako i samo ako je n epsp(b). |
Dokaz: U ovom slučaju je s = 1, t = (n-1)/2. Ako je n epsp(b), onda je
bt
≡
b(n -1)/2
≡
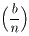 ≡
±1 mod (n),
≡
±1 mod (n),
Neka je sada n spsp(b). To znači da je b(n -1)/2 ≡ ±1 (mod n). Budući da je n ≡ 3 (mod 4), to je (±1/n) = ±1, pa je
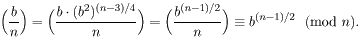
■
| Teorem 4.4: Neka je n neparan složen broj. Tada je n jaki pseudoprosti broj u bazi b za najviše 25% baza b, 0 < b < n. |
Dokaz:
1. slučaj: n nije kvadratno slobodan
Neka je n = p2q, gdje je p
prost. Ako je n spsp(b), onda
je n i psp(b). Pretpostavimo da je
bn -1
≡ 1 (mod n).
Tada je i
bn -1
≡ 1
(mod p2). Po
Lemi 4.1, ova kongruencija ima d =
(p(p -1), n -1) rješenja.
Budući da p|n, to
p ∤ (n -1),
pa p ∤ d.
Zato je d ≤
p -1. Stoga je broj baza b za koje je
n psp(b)
≤ dq ≤ (p -1)q = (p2 -1)q/(p+1) < n/4.
2. slučaj: n = pq, gdje su p i q različiti prosti brojevi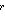 t
≡ -1 (mod p) za neki
r, 0 ≤
r < s. Po Lemi 4.1, ova kongruencija ima rješenja
ako i samo ako je r < u, a broj rješenja je
t
≡ -1 (mod p) za neki
r, 0 ≤
r < s. Po Lemi 4.1, ova kongruencija ima rješenja
ako i samo ako je r < u, a broj rješenja je

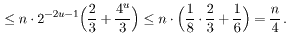
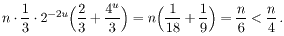
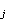 tj,
tj neparan. Postupimo kao u 2.
slučaju. Možemo pretpostaviti da je s1
≥ sj, za sve j. Dobivamo sljedeću
ocjenu za broj baza b takvih da je n spsp(b):
tj,
tj neparan. Postupimo kao u 2.
slučaju. Možemo pretpostaviti da je s1
≥ sj, za sve j. Dobivamo sljedeću
ocjenu za broj baza b takvih da je n spsp(b):

■
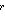
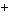
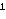 t
≡ 1 (mod n),
t
≡ 1 (mod n),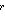 t
≢ -1 (mod n),
t
≢ -1 (mod n),
Napomena: Uz pretpostavku da vrijedi tzv. generalizirana
Riemannova hipoteza (GRH), Miller-Rabinov test postaje
polinomijalni deterministički test. Naime, može se
pokazati da ako je GRH točna i ako je n složen broj,
onda mora postojati barem jedna baza
| Web stranica kolegija Kriptografija | Andrej Dujella - osobna stranica |