[Prethodna tema]
[Sljedeća tema]
5. Eliptičke
krivulje nad konačnim poljima
5.1. Konačna polja
Kod primjena u kriptografiji, eliptičke krivulje se
promatraju nad konačnim poljima. Podsjetimo se osnovnih
svojstava konačnih polja.
Konačno polje s q elemenata označava se s

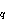 .
Neka je p karakteristika polja
.
Neka je p karakteristika polja

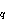 .
Tada
.
Tada 
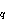 sadrži prosto polje
sadrži prosto polje

 =
=

 ,
i stoga je
,
i stoga je

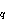 vektorski prostor nad
vektorski prostor nad

 .
Dimenziju od
.
Dimenziju od 
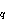 kao vektorskog prostora nad
kao vektorskog prostora nad

 označimo s k. Tada
označimo s k. Tada 
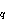 ima pk elemenata, tj.
q = pk.
Nadalje, za svaku potenciju prostog broja
q = pk
postoji jedinstveno (do na izomorfizam) polje s q elemenata.
Jedna od realizacija tog polja je
ima pk elemenata, tj.
q = pk.
Nadalje, za svaku potenciju prostog broja
q = pk
postoji jedinstveno (do na izomorfizam) polje s q elemenata.
Jedna od realizacija tog polja je

 [x] /
(f(x)), gdje je f(x) neki ireducubilni
polinom stupnja k nad
[x] /
(f(x)), gdje je f(x) neki ireducubilni
polinom stupnja k nad 
 .
Elementi ovog polja su polinomi nad
.
Elementi ovog polja su polinomi nad

 stupnja manjeg ili jednakog k - 1 (očito je da takvih polinoma
ima točno pk), dok su operacije
zbrajanje i množenje polinoma u
stupnja manjeg ili jednakog k - 1 (očito je da takvih polinoma
ima točno pk), dok su operacije
zbrajanje i množenje polinoma u

 [x],
s time da se nakon množenja računa ostatak pri
djeljenju s polinomom f(x).
[x],
s time da se nakon množenja računa ostatak pri
djeljenju s polinomom f(x).
Primjer: Konstrukcija polja
 9.
9.
Polinom f(x) =
x2 + 1 je ireducibilan nad
 3
jer nema korijena u
3
jer nema korijena u  3.
Stoga
3.
Stoga
 9
možemo reprezentirati kao
9
možemo reprezentirati kao
 3[x] /
(f(x)). Dakle, elementi od
3[x] /
(f(x)). Dakle, elementi od
 9 su
0, 1, 2, x, x + 1, x + 2, 2x,
2x + 1, 2x + 2. Izračunajmo, na primjer,
(x + 1)2 u polju
9 su
0, 1, 2, x, x + 1, x + 2, 2x,
2x + 1, 2x + 2. Izračunajmo, na primjer,
(x + 1)2 u polju  9.
Imamo: (x + 1)2 = x2 +
2x + 1 = 2x.
9.
Imamo: (x + 1)2 = x2 +
2x + 1 = 2x.
Označimo s 
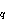 *
multiplikativnu grupu polja
*
multiplikativnu grupu polja

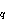 .
Tada je grupa
.
Tada je grupa 
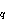 *
ciklička, što znači da postoji element g
*
ciklička, što znači da postoji element g
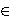

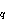 takav da se svaki element iz
takav da se svaki element iz

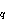 *
može dobiti kao neka potencija od g.
*
može dobiti kao neka potencija od g.
Za primjene u kriptografiji, posebno za primjene eliptičkih krivulja
u kriptografiji, najvažniji su slučajevi kad je q =
p prost broj, te kad je q = 2m
potencija broja 2. Kako smo već rekli, polje
 2
2 jest vektorski
prostor nad
jest vektorski
prostor nad
 2
dimenzije m. Postoji mnogo različitih baza tog vektorskog
prostora. Mi ćemo spomeniti dva tipa takvih baza:
trinomijalne baze i normalne baze.
2
dimenzije m. Postoji mnogo različitih baza tog vektorskog
prostora. Mi ćemo spomeniti dva tipa takvih baza:
trinomijalne baze i normalne baze.
Ako je f(x) ireducibilni polinom stupnja m
nad  2,
tada se polje
2,
tada se polje
 2
2 može reprezentirati kao skup svih polinoma nad
može reprezentirati kao skup svih polinoma nad
 2
stupnja manjeg
od m, s operacijama modulo f(x).
To se zove reprezentacija pomoću polinomijalne
baze. Reprezentacija pomoću trinomijalne baze je
specijalni slučaj reprezentacije pomoću polinomijalne baze u
kojem polinom f(x) ima oblik f(x) =
xm + xk + 1.
Prednost takve reprezentacije jest efikasnost provođenja
redukcije modulo f(x). Za neke m-ove (npr. za
m
2
stupnja manjeg
od m, s operacijama modulo f(x).
To se zove reprezentacija pomoću polinomijalne
baze. Reprezentacija pomoću trinomijalne baze je
specijalni slučaj reprezentacije pomoću polinomijalne baze u
kojem polinom f(x) ima oblik f(x) =
xm + xk + 1.
Prednost takve reprezentacije jest efikasnost provođenja
redukcije modulo f(x). Za neke m-ove (npr. za
m 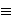 0
(mod 8)), trinomijalna baza ne postoji. Eksperimentalno je pokazano
da trinomijalna baza postoji za nešto više od pola m-ova
manjih od 1000.
0
(mod 8)), trinomijalna baza ne postoji. Eksperimentalno je pokazano
da trinomijalna baza postoji za nešto više od pola m-ova
manjih od 1000.
Normalna baza od
 2
2 nad
nad  2
je baza oblika
2
je baza oblika
{b, b2,
b2 ,
... , b2
,
... , b2

 },
},
gdje je b 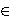
 2
2 . Takva baza uvijek
postoji. U reprezentaciji pomoću normalne baze, kvadriranje
u polju postaje trivijalno: ako je a =
(a0, a1, ... ,
am -1), onda je a2 =
(am -1, a0,
a1, ... , am -2).
Dakle, kvadriranje nije ništa drugo nego ciklički pomak udesno.
Međutim, za općenitu normalnu bazu, množenje u polju je znatno
kompliciranije. Stoga su od interesa one normalne baze kod kojih
je množenje što jednostavnije. Takve baze se nazivaju
optimalne normalne baze (ONB). Optimalna normalna baza
ne mora postojati. Jedan od nužnih uvjeta za postojanje ONB je
da je barem jedan od brojeva n + 1, 2n + 1 prost.
. Takva baza uvijek
postoji. U reprezentaciji pomoću normalne baze, kvadriranje
u polju postaje trivijalno: ako je a =
(a0, a1, ... ,
am -1), onda je a2 =
(am -1, a0,
a1, ... , am -2).
Dakle, kvadriranje nije ništa drugo nego ciklički pomak udesno.
Međutim, za općenitu normalnu bazu, množenje u polju je znatno
kompliciranije. Stoga su od interesa one normalne baze kod kojih
je množenje što jednostavnije. Takve baze se nazivaju
optimalne normalne baze (ONB). Optimalna normalna baza
ne mora postojati. Jedan od nužnih uvjeta za postojanje ONB je
da je barem jedan od brojeva n + 1, 2n + 1 prost.
Zadatci:
- Dokažite da je polinom f(x) =
x3 + x + 1 ireducibilan nad
 2.
Napravite tablice zbrajanja i množenja za 8 elemenata polja
2.
Napravite tablice zbrajanja i množenja za 8 elemenata polja
 8
reprezentiranog kao
8
reprezentiranog kao
 2[x] /
(f(x)).
2[x] /
(f(x)).
- Neka je f(x) = xm +
xk + 1, te neka je
a(x) =
a0 + a1x + a2x2 + ... +
a2m -2x2m -2
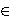
 2[x].
Uvjerite se da sljedeći algoritam računa ostatak pri
dijeljenju polinoma a(x) s polinomom f(x):
2[x].
Uvjerite se da sljedeći algoritam računa ostatak pri
dijeljenju polinoma a(x) s polinomom f(x):
For i = 2m - 2
to m
by -1 do
ai - m = ai - m +
ai
ai - m + k =
ai - m + k + ai.
[Prethodna tema]
[Sljedeća tema]

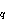 .
Neka je p karakteristika polja
.
Neka je p karakteristika polja

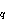 .
Tada
.
Tada 
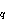 sadrži prosto polje
sadrži prosto polje

 =
=

 ,
i stoga je
,
i stoga je

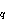 vektorski prostor nad
vektorski prostor nad

 .
Dimenziju od
.
Dimenziju od 
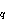 kao vektorskog prostora nad
kao vektorskog prostora nad

 označimo s k. Tada
označimo s k. Tada 
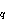 ima pk elemenata, tj.
q = pk.
Nadalje, za svaku potenciju prostog broja
q = pk
postoji jedinstveno (do na izomorfizam) polje s q elemenata.
Jedna od realizacija tog polja je
ima pk elemenata, tj.
q = pk.
Nadalje, za svaku potenciju prostog broja
q = pk
postoji jedinstveno (do na izomorfizam) polje s q elemenata.
Jedna od realizacija tog polja je

 [x] /
(f(x)), gdje je f(x) neki ireducubilni
polinom stupnja k nad
[x] /
(f(x)), gdje je f(x) neki ireducubilni
polinom stupnja k nad 
 .
Elementi ovog polja su polinomi nad
.
Elementi ovog polja su polinomi nad

 stupnja manjeg ili jednakog k - 1 (očito je da takvih polinoma
ima točno pk), dok su operacije
zbrajanje i množenje polinoma u
stupnja manjeg ili jednakog k - 1 (očito je da takvih polinoma
ima točno pk), dok su operacije
zbrajanje i množenje polinoma u

 [x],
s time da se nakon množenja računa ostatak pri
djeljenju s polinomom f(x).
[x],
s time da se nakon množenja računa ostatak pri
djeljenju s polinomom f(x).
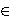
 jest vektorski
prostor nad
jest vektorski
prostor nad
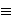 0
(mod 8)), trinomijalna baza ne postoji. Eksperimentalno je pokazano
da trinomijalna baza postoji za nešto više od pola m-ova
manjih od 1000.
0
(mod 8)), trinomijalna baza ne postoji. Eksperimentalno je pokazano
da trinomijalna baza postoji za nešto više od pola m-ova
manjih od 1000.
 ,
... , b2
,
... , b2

 },
},