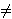 2, 3) postaje
2, 3) postaje
[k] P = P + P + ... + P (k pribrojnika).
Iz formula za zbrajanje točaka vidimo da u slučaju kada je P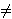 Q,
računanje koordinata točke P + Q zahtijeva
jedno računanje inverza u polju, te tri množenja u polju
(1I + 3M) (zanemarujemo "trošak" za zbrajanje u polju, te množenje
malim konstantama). Kada je P = Q, onda je trošak
za udvostručavanje točke jednak 1I + 4M.
Q,
računanje koordinata točke P + Q zahtijeva
jedno računanje inverza u polju, te tri množenja u polju
(1I + 3M) (zanemarujemo "trošak" za zbrajanje u polju, te množenje
malim konstantama). Kada je P = Q, onda je trošak
za udvostručavanje točke jednak 1I + 4M. 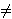 2, 3. Ako je char = 2,
situacija je slična, osim što je u tom slučaju trošak kvadriranja
zanemariv u odnosnu na obično množenje, pa zato dobivamo 1I + 2M.
2, 3. Ako je char = 2,
situacija je slična, osim što je u tom slučaju trošak kvadriranja
zanemariv u odnosnu na obično množenje, pa zato dobivamo 1I + 2M.
Inverz u konačnom polju se računa pomoću Euklidovog algoritma.
Iako je njegova kompleksnost teoretski usporediva s
kompleksnošću množenja, u praksi je množenje ipak dosta
brže od računanja inverza.
Računanje inverza u polju može se izbjeći uvođenjem
težinskih projektivnih koordinata, gdje
(X, Y, Z) odgovara
(X / Z2, Y / Z3).
Tada jednadžba eliptičke krivulje (za char
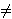 2, 3) postaje
2, 3) postaje
Y2 = X3 + aXZ4 + bZ6.
Sada se kod računanja zbroja dvaju točaka uopće ne pojavljuje djeljenje. Na taj način, trošak za računanje P + Q postaje 16M, a za računanje [2]P trošak je 10M. Na primjer, koordinate točke (X2, Y2, Z2) = [2] (X, Y, Z) se mogu izračunati na sljedeći način:
m1 = 3X2 + aZ4,
m2 = 4XY2,
m3 = Y4,
X2 = (m1)2
- 2m2,
Y2 = m1(m2
- X2) - m3,
Z2 = 2YZ.
Računanje višekratnika točke na eliptičkoj krivulji, specijalni
je slučaj općeg problema potenciranja u abelovoj grupi.
Stoga se mogu primijeniti razni algoritmi koji su poznati za
taj opći problem.
Najjednostavnija (i najstarija) efikasna metoda za računanje višekratnika točaka koristi binarni zapis broja k. Zove se binarna metoda ili metoda uzastopnog kvadriranja. Na primjer, binarni zapis broja 100 je (1100100)2. Sada točku [100] P možemo izračunati kao [2]([2](P + [2]([2]([2](P + [2]P))))).
|
ALGORITAM: INPUT: točka P i g-bitni prirodni broj k = 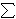 kj 2j,
kj
kj 2j,
kj 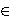 {0,1}
{0,1} OUTPUT: točka Q = [k] P
|
Broj "bitnih" operacija za računanje [k] P pomoću ovog algoritma je O(log k log3 q).
Poznato je više općih poboljšanja binarne metode. Međutim,
postoji je jedno poboljšanje koje je prilično specifično za
eliptičke krivulje. Naime, za razliku od nekih drugih grupa,
kod eliptičkih krivulja inverzna operacija (oduzimanje)
ima doslovno isti trošak kao i originalna grupovna operacija
(zbrajanje). To je zbog toga što vrijedi
-(x, y) = (x, -y) za char
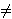 2, dok je
-(x, y) = (x, x + y) za char = 2.
2, dok je
-(x, y) = (x, x + y) za char = 2.
Ova činjenica nas motivira za umjesto binarnog prikaza
broja k, koristimo tzv. SD (signed digit) prikaz
oblika
k =
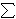 sj 2j,
kj
sj 2j,
kj 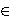 {-1,0,1}.
Jasno je da ovakav prikaz nije jedinstven. Npr. 3 = (0 1 1) =
(1 0 -1). Stoga možemo pokušati izabrati prikaz koji će voditi
do što efikasnijeg algoritma. Reći ćemo da je SD prikaz
rijedak ili nesusjedni (non-adjacent form, NAF)
ako nema susjednih znamenaka različitih od 0, tj. ako je
sj sj+1 = 0,
za svaki j. Poznato je da svaki prirodan broj k ima
jedinstveni NAF, te da NAF ima najmanju težinu (broj
sj-tova različitih od 0), među svim
SD prikazima od k. Očekivana težina NAF-a je g/3,
za razliku od binarnog prikaza kod kojeg je očekivana težina
g/2.
{-1,0,1}.
Jasno je da ovakav prikaz nije jedinstven. Npr. 3 = (0 1 1) =
(1 0 -1). Stoga možemo pokušati izabrati prikaz koji će voditi
do što efikasnijeg algoritma. Reći ćemo da je SD prikaz
rijedak ili nesusjedni (non-adjacent form, NAF)
ako nema susjednih znamenaka različitih od 0, tj. ako je
sj sj+1 = 0,
za svaki j. Poznato je da svaki prirodan broj k ima
jedinstveni NAF, te da NAF ima najmanju težinu (broj
sj-tova različitih od 0), među svim
SD prikazima od k. Očekivana težina NAF-a je g/3,
za razliku od binarnog prikaza kod kojeg je očekivana težina
g/2.
 751.
Izračunajte [100] P.
751.
Izračunajte [100] P.
c0 = 0
For j = 0 to g do
cj + 1 =(kj + kj + 1 + cj) / 2
![]](symbols/rfloor.gif)
sj = kj + cj - 2cj + 1.
| Web stranica seminara | Andrej Dujella - osobna stranica |