Ovo je tekst clanka napisanog
07.12.1998. na poziv glavnog urednika jednog casopisa. Clanak
nije nikada objavljen niti u jednom casopisu pa ga ovdje
objavljujem kao zabavno i poucno stivo za ljetnu razbibrigu u
debeloj hladovini.
Igra kojom
upravlja kompjutor!
UVOD
Zvuči privlačno i inovativno.
Stoga se jedna igra i reklamira u najmoćnijem mediju
današnjice, televiziji, upravo tim sloganom. O toj igri bit će
riječi u ovom članku. No prije toga, pogledajmo malo oko sebe,
u kakvom svijetu živimo.
Danas računala upravljaju baš
svime: lansiranjem raketa, avionskim letovima, proizvodnim
procesima, telekomunikacijskim sustavima, vojnim operacijama,
prometnim sustavima, sustavima zaštite objekata i tako redom,
sve do jednostavnijih uređaja kao što su primjerice
programabilni šivaći stroj ili mikrovalna pećnica. Stoga, na
prvi pogled, nema ništa neobično u činjenici da nekom
nagradnom igrom upravlja baš računalo. Prisjetimo se, danas
uobičajenog, praćenja sportskih događaja raznim važnim i nevažnim statistikama koje zaslugom
računala u trenutku stižu u naše domove. No, tu se radi o
nečem drugom, odnosno računalo ovdje služi za kvalitetnije praćenje
igre a ne za upravljanje
igrom. Prema tome, u naslovnoj rečenici su, na vješt način,
iskombinirani dijelovi pojmova upravljanja
procesima i praćenja igre, čime dolazimo do novog pojma upravljanje
igrom. Upravljanje igrom
može se zvati i namještanje rezultata igre. U dijelu
ekshibicijskih mečeva, čija je glavna zadaća promičba
određenog sporta, rezultati su unaprijed poznati organizatorima
i u tome zapravo nema ničeg lošeg.
Zbog čega upravljanje procesom
općenito smatram poželjnim a upravljanje igrom nepoželjnim?
Stoga, što se upravljanjem procesom općenito postižu željeni
rezultati. Primjerice, kruh se peče točno određeno vrijeme, ne
ostaje gnjecav niti pretvrd, što je dobro. Avioni slijeću
točno na slijetne piste, ne sudaraju se međusobno u zraku i ne
oštećuju vrhove planina, što je također dobro. Automobili i
pješaci se prolaskom tijekom upaljenog zelenog svjetla uspješno mimoilaze na
križanjima, što je posebno dobro. No, igra u kojoj se pobjednik
unaprijed zna zapravo ne postoji, budući da se takva igra nema
pravo zvati igrom već predstavom. Nipošto ne tvrdim da takve
predstave ne mogu biti zabavne (primjerice wrestling) ali o stvarnoj neizvjesnosti takvih
igara ne može biti govora.
ZAPLET
Sredinom studenog, dakle tri
tjedna prije pisanja ovog članka a barem šest tjedana prije
nego što ćete vi ovaj članak imati priliku pročitati,
najčitaniji list je pokrenuo igru, nazovimo je I, u kojoj je dobitnik unaprijed određen.
Pojednostavnjeno govoreći, unaprijed su zadani veliki skup G={g1,
g2,…, gn} gubitnih kupona i mali skup
D={d1, d2,…, dm} dobitnih
kupona. Preostala pravila igre I su vrlo jednostavna. Tko
ima dobitni kupon, dobiva nagradu, a tko ima gubitni kupon, ne
dobiva ništa.
Priznajte da vas, ovako zapisano,
igra pomalo podsjeća na igre gdje se ispod zatvarača boca, ili
u zatvorenim vrećicama kriju razne primamljive nagrade. Prema
svemu do sada napisanom, čini se da bitne razlike između ove
dvije igre i nema. Pa ipak, razlika ipak postoji. Naime,
kupujući bocu s nagradnim zatvaračem (ili zatvorenu vrećicu),
prije zavirivanja pod zatvarač (ili u vrećicu), igrač je
svjestan činjenice da je nagradni predmet (zatvarač ili vrećica) sa željenom
nagradom možda izišao (a možda i nije) s mjesta gdje je
stvoren. To je trajan problem svih sličnih igara i molim
organizatore svih sličnih promotivnih igara da se ne nađu
povrijeđeni, jer morao sam za primjer usporedbe uzeti neki primjer iz stvarnog života.
U našoj, gore spomenutoj igri I, zbog nepotpuno izrečenih pravila,
sudionici igre u početku imaju dojam kao da igra I nalikuje na (izmišljenu) igru loto 3/90.
Naime u jednoj tročlanoj kombinaciji treba pogoditi tri
izvučena broja. Izvlači se 56 od 90 brojeva. Prema tome, ako se
na bilo kojoj kombinaciji (a za ciglih pet kuna dobiva se čak
trideset kombinacija s kojima se ravnopravno sudjeluje u igri)
pojave bilo koja tri broja od 56 izvučenih, dobitak je osvojen.
KULMINACIJA
Fantastično! Dakle, imamo 30
tročlanih kombinacija na jednom kuponu, izvlači se 56 brojeva
od 90 i ako imamo u jednoj kombinaciji tri izvučena broja,
nagrada je naša. Da vidimo kolike su nam šanse za uspjeh.
Račun koji provodim ne dovodi do najapsurdnijeg rezultata koji
je moguće postići uz dane pretpostavke (u matematičkom smislu)
ali je, pretpostavljam, najbliži načinu razmišljanja
razboritog loto igrača..
Prema tome, na posao. Svi
loto-matematičari znaju da se od 90 brojeva može napraviti 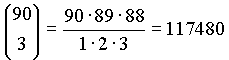 različitih trojki (tročlanih
podskupova). Na isti način, loto-matematičari, bez obzira
voljeli matematiku ili ne, znaju da 56 dobitnih brojeva daje
različitih trojki (tročlanih
podskupova). Na isti način, loto-matematičari, bez obzira
voljeli matematiku ili ne, znaju da 56 dobitnih brojeva daje 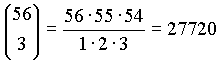 dobitnih kombinacija. Nadalje,
zaključujemo da su šanse za dobitak na samo jednoj
kombinaciji jednake
dobitnih kombinacija. Nadalje,
zaključujemo da su šanse za dobitak na samo jednoj
kombinaciji jednake 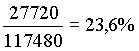 . A zamislite tek na 30 kombinacija!
Stoga, navalimo na kupovinu kupona. Bez daljnjeg računa, samo
procjenom, igrač jednostavno “mora” zaključiti da nakon
kupovine 11 kupona “nema šanse” da nešto ne dobije. Na isti
način zaključuju i drugi, treći, tisućiti, desettisućiti, pa
čak i pedesettisućiti igrač. Dakle, evo konačno igre u kojoj
svi dobivaju ili barem tako misle.
. A zamislite tek na 30 kombinacija!
Stoga, navalimo na kupovinu kupona. Bez daljnjeg računa, samo
procjenom, igrač jednostavno “mora” zaključiti da nakon
kupovine 11 kupona “nema šanse” da nešto ne dobije. Na isti
način zaključuju i drugi, treći, tisućiti, desettisućiti, pa
čak i pedesettisućiti igrač. Dakle, evo konačno igre u kojoj
svi dobivaju ili barem tako misle.
RASPLET
No, dani prolaze, izvučeni
brojevi se neposlušno razmiču po kuponima i nikako se ne mogu
naći barem tri broja koji bi sretno živjeli u istoj
kombinaciji. Zašto?
Zato, jer kupci kupona, sudionici igre I, zapravo i nisu kupovali kupone s po 30
potencijalnih dobitnih tročlanih kombinacija, već kupone s
otisnutim slovima iz skupa {g1, g2,…,
gn,d1, d2,…, dm}.
Slova g1, g2,…, gn, d1,d2,…,
dm nažalost (ili na
sreću) igračima nisu bila vidljiva. Ali su se mogla (lako ili
teško – kako kome) rekonstruirati poznavanjem sadržaja šest
različitih nedobitnih kupona i poznavanjem četiri izvučena
broja. Na tu činjenicu sam upozorio 28.11.1998. Web stranicom www.math.hr/~igaly/spojii.htm. Izvorni kod programa za određivanje
dobitnih brojeva poznavanjem ovog skupa ulaznih podataka, pisanog
u programskom jeziku C, možda je danas dostupan na adresi www.math.hr/~igaly/vl3b.htm. Smatram da ovaj problem može poslužiti
kao lijep primjer korištenja tehnike rekurzivnog programiranja,
te se njime može testirati kako umješnost programera, tako i
kvaliteta korištenog C-prevoditelja. Problem određivanja 56
dobitnih brojeva uz ranije navedene uvjete spada u klasu problema
pokrivanja kao što su npr.: problem smještanja 8 dama na
šahovsku ploču tako da se međusobno ne napadaju ili problem popločavanja
šahovske ploče sa svih 12 pentomina.
Ponovimo još jednom, za one koji još nisu sudjelovali u
opisanoj igri I, čime do
sada raspolažemo: Kupnjom 6 kupona, te korištenjem programa za
računalo, odredili smo, u prihvatljivom roku, sve dobitne
brojeve, odnosno pomoću tih brojeva mogli smo za svaki kupon
odmah reći dobiva li ili ne. Razlog tome leži zapravo u
činjenici da je ranije izračunata vjerojatnost dobitka po
jednoj kombinaciji (23,6%) puno prevelika da bi se lako, bez puno namještanja, svim kombinacijama
jednog kupona mogao uskratiti dobitak. Posebni problemi za
organizatora nastaju u trenutku kad treba generirati puno
različitih kupona koji ne smiju nalikovati jedan na drugoga.
Naime, kad bi kuponi smjeli jako nalikovati jedan na drugoga, posao
organizatora bio bi u mnogo čemu olakšan, a kad bi tek svi
gubitni kuponi smjeli biti isti, to bi posebno olakšalo posao
organizatoru, no vjerojatno bi izazvalo i izvjesnu sumnju
natjecatelja. O prijedlogu slične igre pišem u zadnjem dijelu ovog članka.
Dakle, već prvog dana igre su
svi igrači mogli za sve kupone znati jesu li dobitni ili ne. Tu
prestaje draž igre i neizvjesnost koja je trebala trajati 14
dana, tijekom kojih su se, malo po malo, trebale dijeliti
nagrade, od manjih prema većima.
Dok ovo čitate, u tijeku će
biti već i četvrto kolo igre I, s igračima željnim dobitka koji im je
cijelo vrijeme nadomak ruke, ali im uvijek promakne za dlaku.
Koliko me sjećanje služi, u razdoblju između organiziranih
lanaca sreće i financijskih inženjeringa je, u našem dnevniku
s najvećom nakladom, objavljen vrlo kvalitetan podlistak o
sociološkoj pozadini igara na sreću u kojem je vrlo lijepo
izloženo koji sve uvjeti u društvu moraju biti zadovoljeni pa
da neka igra dosegne veliku popularnost. Stoga se ja ovdje
ne bavim tom problematikom.
U određenom krugovima ljudi,
srž igre I je već
razotkrivena, no većina ljudi koji su se uvjerili u točnost
mojih predviđanja izvučenih brojeva, i dalje će mi uporno
postavljati isto pitanje: “Ako možete predvidjeti
dobitne brojeve igre I,
možete li odrediti i dobitne brojeve za loto?”. Nažalost,
takvima ne mogu pomoći.
ZAKLJUČAK
Za kraj, imam nekoliko prijedloga
za organizatore igara na sreću. Igre su rađene po uzoru na neke
ranije poznate, a nekima je kao uzor poslužila upravo igra I. U svakoj od njih je bitno da je skup
igrača unaprijed podijeljen na dobitnike i gubitnike, kraće D i
G.
Igra prva
Ovo je tipična kockarska igra za
dva igrača. Liči na igru par-nepar ali se malo razlikuje.
Dakle, G i D ulože određenu količinu novca. Svaki igrač
izgovara jedan broj. Koji igrač izgovori veći broj, pobjednik
je. Prvi broj izgovara G, a nakon njega to čini D.
Igra druga
Ovu igru, za razliku od
prethodne, igra puno igrača – što više – to bolje. Dijeli
se 10 privlačnih nagrada. Tiskano je 10 plastificiranih kartica
s brojevima od 1 do 10, te 100000 istih takvih plastificiranih
kartica, ali s brojem 0. D prvi kupuju kartice a nakon njih to
isto čine G. Nagrade se dodjeljuju onim sudionicima igre koji
imaju na kartici neki broj
između 1 i 10.
Igra treća
Ova igra je jedna varijacija na
temu poznate igre sa šibicama koja se obično igra u vlakovima
koji često staju na postajama.
D ima tri kutije šibica, otvorom okrenutim prema dolje. Ispod
jedne kutije stavlja neki sitan
predmet (novčić, šibicu ili slično). Pokretima ruke D
zamiješa kutije, ali tako da G može cijelo vrijeme nesmetano
nadzirati postupak. Zatim D jednu kutiju privuče k sebi i
omogući G pogađanje ispod koje od preostale dvije kutije se
traženi predmet nalazi. Ako G pogodi, dobiva 1000000
kuna, a ako ne, D dobiva 5 kuna.
Igra četvrta
Ovo je prijedlog za
pojednostavnjenje igre loto 7/39. Loto listići su unaprijed
ispunjeni. Svaki G može kupiti listića koliko želi i ne mora
ništa više raditi. Na svim uplatnim mjestima je objavljen popis
dobitnih brojeva koji će biti izvučeni u tom kolu: 5, 14, 18,
19, 22, 32 i 39. Određenog dana u tjednu, D organizira javno
izvlačenje i lijepa hostesa govori sljedeći tekst: “Sada u
bubanj stavljamo brojeve 18, 32, 14, 5, 22, 19 i 39. Molim povjerenstvo da provjeri je
li svih 7 navedenih brojeva u bubnju”. Uz glazbu i vidljivo
uzbuđenje u gledalištu, izvlači se redom svih 7 ranije
ubačenih brojeva. Veliku nagradu od 5000000 kuna dobiva svaki
onaj G koji na svom listiću ima zaokružen barem jedan izvučeni broj.
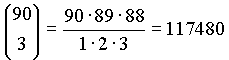 različitih trojki (tročlanih
podskupova). Na isti način, loto-matematičari, bez obzira
voljeli matematiku ili ne, znaju da 56 dobitnih brojeva daje
različitih trojki (tročlanih
podskupova). Na isti način, loto-matematičari, bez obzira
voljeli matematiku ili ne, znaju da 56 dobitnih brojeva daje 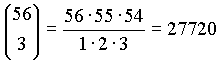 dobitnih kombinacija. Nadalje,
zaključujemo da su šanse za dobitak na samo jednoj
kombinaciji jednake
dobitnih kombinacija. Nadalje,
zaključujemo da su šanse za dobitak na samo jednoj
kombinaciji jednake 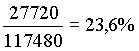 . A zamislite tek na 30 kombinacija!
Stoga, navalimo na kupovinu kupona. Bez daljnjeg računa, samo
procjenom, igrač jednostavno “mora” zaključiti da nakon
kupovine 11 kupona “nema šanse” da nešto ne dobije. Na isti
način zaključuju i drugi, treći, tisućiti, desettisućiti, pa
čak i pedesettisućiti igrač. Dakle, evo konačno igre u kojoj
svi dobivaju ili barem tako misle.
. A zamislite tek na 30 kombinacija!
Stoga, navalimo na kupovinu kupona. Bez daljnjeg računa, samo
procjenom, igrač jednostavno “mora” zaključiti da nakon
kupovine 11 kupona “nema šanse” da nešto ne dobije. Na isti
način zaključuju i drugi, treći, tisućiti, desettisućiti, pa
čak i pedesettisućiti igrač. Dakle, evo konačno igre u kojoj
svi dobivaju ili barem tako misle.